Modelling section lift, drag and pitching moment
The rotor blade section loading actions of interest are the lift, drag and pitching moment. All three are important and all three can signal limiting effects in terms of blade flap, lag and torsion response. A common approximation to real flow effects assumes twodimensional, quasi-steady variations with local incidence and Mach number uniquely determining the blade loading. In Ref. 3.58, Prouty gives an account of empirical findings based on analysis of a wide range of two-dimensional aerofoil test data. Key parameters defining the performance and behaviour of an aerofoil section are the maximum achievable lift coefficient CLmax and the drag divergence Mach number Md. Both depend critically on the geometry of the aerofoil, as expected, and hence on the type of rotor stall. Prouty identifies three types of stall to which rotor blades are prone – thin aerofoil, leading edge and trailing edge stall.
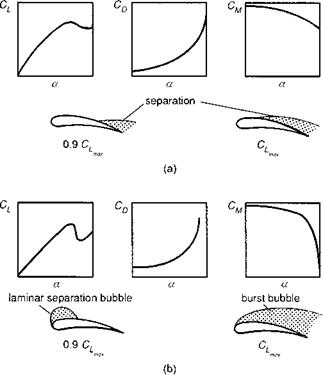
Prouty’s findings suggest that aerofoil sections with thickness-to-chord ratios greater than about 8% will normally experience trailing edge stall and, at their best, achieve values of CLmax up to about 1.6. For thinner aerofoils, leading edge stall is more likely, with a CLmax that increases with thickness/chord up to about 1.8. The general effects of trailing and leading edge stall on lift, drag and moment coefficients are sketched in Fig. 3.41, where these are shown as functions of incidence.
|
Fig. 3.41 Types of aerofoil stall: (a) trailing edge stall; (b) leading edge stall |
Trailing edge stall is characterized by a gradual increase in the region of separated flow moving forward from the trailing edge. Leading edge stall is triggered by the bursting of a laminar separation bubble over the nose of the aerofoil giving rise to sharp changes in lift, drag and pitching moment. Generally, thin aerofoils are favoured for their performance (high Md) at high Mach number on the advancing side of the disc, and thicker aerofoils are favoured for their performance (high C^max) at low Mach number and high incidence on the retreating side. Most helicopter blades are therefore designed as a compromise between these two conflicting requirements and may experience both types of stall within the operating envelope. Reference 3.59 describes the evolution of the cambered aerofoil sections adopted for the Lynx helicopter, showing a favourable all-round comparison with the thicker, symmetrical NACA 0012 section. The latter was typical of aerofoil sections used on helicopter rotors before the 1970s.
In blade element rotor simulation models, the lift, drag and pitching moment coefficients are usually stored in table look-up form as nonlinear functions of incidence and Mach number, with the data tables derived from either wind tunnel tests or theoretical predictions. In Ref. 3.6, Bramwell reports on the effects of swirl and other three-dimensional, in-plane effects on section characteristics with significant changes in Cimax particularly at the higher Mach numbers. Also, in Ref. 3.60, Leishman draws attention to the powerful effects of sweep angle on CLmax. Generally, however, for a large extent of the rotor radius, the two-dimensional approximation is relatively accurate. An exception is close to the tip, where three-dimensional effects due to the interaction of the upper and lower surface flows result in marked changes in the chord – wise pressure distribution for a given incidence and Mach number. Accurate modelling of the tip aerodynamics is still the subject of intense research and renewed impetus with the advent of novel tip sections and planforms.
In forward flight and manoeuvres, the section incidence and Mach number are changing continuously and we need to consider the effects of aerodynamic unsteadiness on the section characteristics. In a series of papers (e. g., Refs 3.61 – 3.64) Beddoes and Leishman have reported the development of an indicial theory for unsteady compressible aerodynamics applicable to both attached and separated flow, for the computation of section lift, drag and pitching moment. In attached flow, the shed wake in the vicinity of the aerofoil induces a time-dependent circulatory force on the section, with a transient growth corresponding to about five chord lengths. A non-circulatory lift also develops (due to the airfoil virtual mass) and decays to zero in approximately the same spatial scale. Both effects are approximated in the Beddoes model by combinations of exponential functions (Ref. 3.63) responding to arbitrary motions of an aerofoil in pitch and heave. To account for the response of the aerofoil to its passage through the wake and individual vortices of other blades, the method also models the loading actions due to arbitrary variations in the incidence of the airflow (Ref. 3.64). A special feature of these developments has been the extension to the modelling of separated flow and the prediction of dynamic stall (see earlier paper by Johnson and Ham for discussion of the physics of dynamic stall, Ref. 3.65). In unsteady motion, the passage of shed vorticity over the aerofoil upper surface following leading edge stall gives rise to a delay in both lift and moment ‘break’, resulting in an overshoot of lift to well beyond the normal quasi-steady value of Cimax. Beddoes has encapsulated this effect in a semi-empirical model, summarized in Fig. 3.42, taken from Ref. 3.62. To quote from Ref. 3.62
|
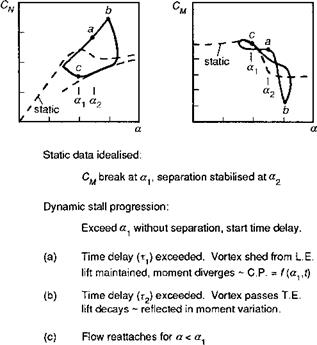
Fig. 3.42 Time delay model for dynamic stall (Ref. 3.62) (T. E., trailing edge; L. E., leading edge; C. P., centre of pressure) |
For each Mach number the angle of attack (a1) which delimits attached flow is determined by the break in pitching moment and a further angle (a2) is used to represent the condition where flow separation and hence centre of pressure is stabilised. In application, when the local value of angle of attack exceeds a1 the onset of separation is assumed to be delayed for a finite period of time (t1) during which the lift and moment behave as appropriate for attached flow. When this time delay is exceeded, flow separation is assumed to be initiated by the shedding of a vortex from the surface of the aerofoil and after a period of time (t2), during which the vortex traverses the chord, it passes free of the surface. In this interval, lift is generated by the vortex and the overall level maintained equivalent to that for fully attached flow but the centre ofpressure moves aft as a function ofboth angle ofattack and time. When the vortex passes free of the surface, the lift decays rapidly to a value appropriate to fully separated flow assuming that the angle of attack is still sufficiently high. Ifand when the angle of attack reduces below the value a1 re-attachment of the flow is represented by the attached flow model, re-initialised to account for the current lift deficiency.
Beddoes goes on to suggest ways that the method can be extended to account for trailing edge stall and also in compressible conditions, when stall is more often triggered by shock wave-boundary layer interaction (Ref. 3.62). Unsteady aerodynamic effects are essential ingredients to understanding many rotor characteristics at high speed and in manoeuvres, and have found practical application in current-generation loads, vibration and aeroelastic stability prediction models. The impact on flight dynamics is less well explored, but two important considerations provide evidence that for some problems, unsteady aerodynamic effects may need to be simulated in real-time applications. First, we consider the azimuthal extent of the development of unsteady lift and moment. The linear potential theory discussed above predicts a time to reach steady-state lift following a step change in incidence of about 5-10 chord lengths, equating to between 10° and 20° azimuth. Even the lower frequency one-per-rev incidence changes associated with cyclic pitch will lead to a not-insignificant phase lag, depending on the rotorspeed. Phase lags as low as 5° between control inputs and lift change can have a significant effect on pitch to roll cross-coupling. Second, modelling the trigger to blade stall correctly is important for simulating flight in gross manoeuvres, when the azimuthal/radial location of initial stall can determine the evolution of the separated flow and hence the effect on pitch and roll hub moments particularly. Dynamic, rather than quasi-steady stall, is, of course, the norm in forward flight and manoeuvring conditions.
With two-dimensional test data tables, three-dimensional and low-frequency unsteady corrections and an empirical stall model, deriving the section forces and pitching moment is a relatively straightforward computational task. A much more significant task is involved in estimating the local incidence.