Wing Geometrical Parameters

Aircraft wings are made up of aerofoil sections, placed along the span. In an aircraft, the geometry of the horizontal and vertical tails, high-lifting devices such as flaps on the wings and tails and control surfaces such as ailerons are also made by placing the aerofoil sections in spanwise combinations.

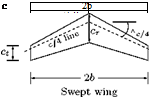
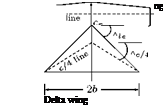
The relevant parameters used to define the aerodynamic characteristics of a wing of rectangular, unswept trapezoidal, swept and delta configurations are illustrated in Figure 4.25.

Wing Area S

This is the plan surface area of the wing. Thus, the representative area of the wing may be regarded as the product of the span (2b) and the average chord (c). Although a portion of the area may be

Figure 4.25 Geometric parameters of some wing planforms.

covered by fuselage, the pressure distribution over the fuselage surface is accounted in the representative wing area.

Wing Span 2b

This is the distance between the tips of port and starboard wings.

Average Chord c

This is the geometric average of the chord distribution over the length of the wing span.

Aspect Ratio Ж

Aspect ratio is the ratio of the span and the average chord. For a rectangular wing, the aspect ratio is:

M =

c

For a nonrectangular wing:

The Ж is a fineness ratio of the wing and it varies from 35 for sailplanes to about 2 for supersonic fighter planes.

Root Chord cr

Root chord is the chord at the wing centerline, that is, at the middle of the span, as shown in Figure 4.25. The tip chordct is the chord at the wing tip.

Taper Ratio X

Taper ratio is the ratio of the tip chord to root chord, for the wing planforms with straight leading and trailing edges.

ct

к =

cr

The taper ratio affects the lift distribution of the wing. A rectangular wing has a taper ratio of 1.0 while the pointed tip delta wing has a taper ratio of 0.0.

Sweep Angle л

Sweep angle is usually measured as the angle between the line of 25% chord and a perpendicular to the root chord. The sweep of a wing affects the changes in maximum lift, the stall characteristics, and the effects of compressibility.

Mean Aerodynamic Chord mac

Mean aerodynamic chord is an average chord which, when multiplied by the product of the average section moment coefficient, the dynamic pressure, and the wing area, gives the moment for the entire wing. The mean aerodynamic chord is given by:

1 f+b

mac = – J [c(y)2dy.

Dihedral Angle

Dihedral angle is the angle between a horizontal plane containing the root chord and a plane midway between the upper and lower surfaces of the wing. If the wing lies below the horizontal plane, it is termed as anhedral angle. The dihedral angle affects the lateral stability of the aircraft.

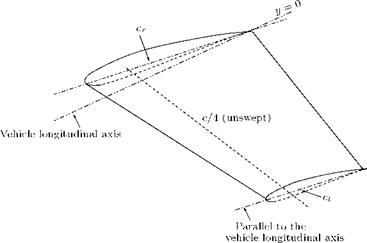
Geometric Twist

Geometric twist defines the situation where the chord lines for the spanwise distribution ofall the aerofoil sections do not lie in the same plane. Thus, there is a spanwise variation in the geometric angle ofincidence for the sections. The chord of the root section of the wing shown in Figure 4.26 is inclined at 4° relative to the vehicle axis.

The chord at the wing tip, however, is parallel to the longitudinal axis of the vehicle. In this case, where the incidence of the aerofoil sections relative to the vehicle axis decrease toward the tip, the wing has a “wash-out.” The wings of most subsonic aircraft have wash-out to control the spanwise lift distribution and, hence, the boundary layer characteristics. If the angle of incidence increases toward wing tip, the wing has “wash-in.”

Example 4.6

For a wing with root chord 18 m, tip chord 3.5 m and span 25 m, calculate the wing area, aspect ratio, taper ratio and the mean aerodynamic chord.

Figure 4.26 Unswept, tapered wing with geometric twist (wash-out).

For calculating the mac, the expression for the chord as a function of the distance from the plane of symmetry is required. The required expression for the given wing is: