Aerodynamic Force and Moment Coefficients

For thin aerofoils at low angle of attack, the lift results mainly from the pressure distribution (that is, pressure forces), as shown in Figure 4.19. The shear forces due to viscosity acts primarily in the chordwise direction and contributes mainly to the drag. Therefore, we need to consider only the pressure contributions, illustrated in Figure 4.27, to calculate the force in the z-direction.

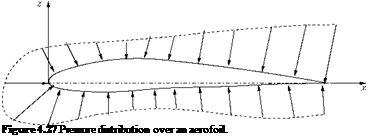Let us consider a wing section in a flow field, as shown in Figure 4.28. Let p be the pressure acting on a differential area (dxdy).

When the boundary layer is thin, the pressure distribution around the aerofoil can be regarded equivalent to that due to an inviscid flow. Thus, the pressure distribution is independent of Reynolds number and

does not depend on whether the boundary layer is laminar or turbulent. When the boundary layer is thin, the pressure coefficient at a particular location on the surface, given by the coordinates (x/c, y/2b), is independent of vehicle scale and of the flow conditions. Over a range of flow conditions for which the pressure coefficient is a unique function of the dimensionless coordinates (x/c, y/2b), the value of the integral equation (4.23) depends only on the aerofoil geometry and the angle of attack. Thus, the resulting dimensionless force coefficient is independent of model scale and flow conditions.

A similar analysis can be used to calculate the lift coefficient, defined as:

(4.24)

where L is the lift and S is the wing planform area.

In the same manner, lift coefficient per unit length of wing span, termed section lift coefficient can be expressed as:

where l is the lift per unit length of wing span and c is the chord length.

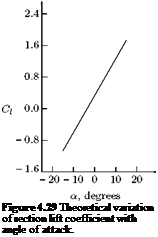
Typical variation of section lift coefficient with angle of attack is shown in Figure 4.29.

It has been experimentally verified that the section lift coefficient is a linear function of angle of attack a from —10° to +10°. The slope of the linear portion of the curve is called the two-dimensional lift curve slope. Theoretical value of two-dimensional lift curve slope is 2n, that is:

-Q

Cl, a — – Q — 2n.
da

The section lift coefficient for a wing which experiences zero lift at a = 0 can be expressed as:

Cl — Cl, aa.

For a wing which experiences zero lift at an angle of a = a0l, the section lift coefficient can be expressed as:

Example 4.7

Air at 300 km/h, 1 atm and 30 °C flows over a two-dimensional rectangular wing of chord 1.2 m. If the zero lift angle of attack for the wing is -2° and Cla = 0.10, calculate the left acting on the wing per unit span when the angle of attack is 3°.

Solution

Given, V = 300/3.6 = 83.33 m/s, p = 101325 Pa, T = 30 + 273.15 = 303.15 K, a0l = -2°, a = 3°. The section coefficient, by Equation (4.26), is:

Cl = Cl, a (a — a0,l)

= 0.10 X (3 — (—2)) = 0.5.

The corresponding lift is:

l = – pV2cC
2 p

The freestream density is:

101325

287 x 303.15 = 1 . 165 kg/m3 .

Therefore:

l = – x 1.165 x 83.332 x 1.2 x 0.5 2