Boundaries with Discontinuities
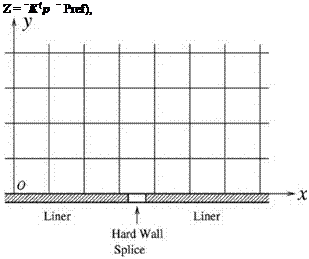
In CAA, one often has to compute acoustic reflections or propagation over surfaces that are made up of different materials. At the junction of two materials, such as shown in Figure 9.14, the incident sound waves encounter a line discontinuity. Computationally, the grid size is, inevitably, finite. Because of the finite size mesh, experience indicates that spurious reflected waves are usually produced. To minimize spurious reflected waves, it is necessary to use a very fine computational mesh. This is sometimes a very costly remedy. It would be ideal to have a method that minimizes such spurious reflected waves without having to refine the computational mesh.
In jet engines, acoustic liners are, invariably, installed on the inside surface of the inlet and exhausted ducts, (see Motsinger and Kraft, 1991; Eversman, 1991). Acoustic liners are the most effective device for the suppression of engine fan noise at the present time. The junction between two acoustical liners with different impedance are examples of surface discontinuity. To facilitate the installation and maintenance of acoustic liners, hard wall splices are introduced. These splices are installed between two pieces of acoustic liners. Their presence creates additional surface discontinuities. To minimize the scattering of acoustic waves by hard wall splices, engine manufacturers resort to the use of very narrow splices. This poses a real dilemma for duct mode computation. In the absence of narrow splices, the use of a computational mesh with 7 to 8 mesh points per wave length in conjunction with a large-stencil CAA algorithm will have enough resolution for the computation. However, with narrow splices, the splice width is sometimes less than the size of a mesh spacing. This is as shown in Figure 9.15. In this case, the hard wall splice is invisible to the computation. Traditional wisdom will call for the use of much finer mesh. A factor of 10 or more mesh size reduction is often deemed necessary. This is to allow 8 to 10 mesh points to lie on the hard wall splice. This is, undoubtedly, very expensive. Not only the number of grid points has to increase substantially, but also the size of the time step used in the computation has to be significantly reduced. It
would, therefore, be extremely useful to have a method that can perform the narrow splice-scattering computation using the original coarse grid without mesh size reduction.
In this section, a method capable of computing acoustic wave propagation and reflection in the presence of surface discontinuities as shown in Figures (9.14) and (9.15) using a large-size computational mesh is discussed. The method is known as the “wave number truncation method” (see Tam and Ju, 2009).
Now consider the wall boundary condition shown in Figure 9.14. On the hard wall side of the junction, the rigid wall boundary condition is
v = 0, (9.61)
where v is the velocity component normal to the wall. Let к be the elastic constant of the elastic wall and Z be the vertical displacement of the surface (positive in the direction of outward-pointing normal), then the elastic wall boundary condition is
(9.62)
Figure 9.15. A narrow splice with width smaller than a grid spacing.
![]()
|
|||
|
|||
|
|||
|
|||
|
|||
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|
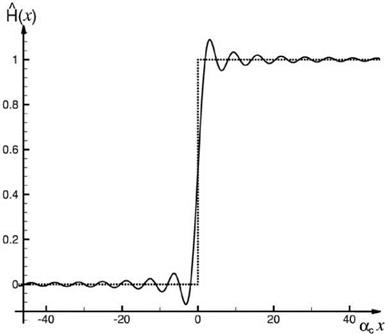
Figure 9.16. The H(x) function. |
Figure 9.16 shows H(x) as a function of acx. Now, it is proposed to use the following modified boundary condition instead of the exact boundary condition (9.64):
v =-к pH(x). (9.69)
at
That is, H (x) is replaced by H (x). The effectiveness and accuracy of the wave number truncation method and its extension (narrow scatterer) will be demonstrated by several examples in the last section of Chapter 10.