An Estimate of the Acceleration of a Lifting Surface in Flight over a Wavy Wall

To evaluate the ride quality of a wing-in-ground-effect vehicle versus the de­sign parameters and the characteristics of waviness of the underlying surface, qualitative analysis will be performed in this paragraph of the acceleration
due to flight of a lifting surface close to wavy solid wall. Assuming for simplic­ity that in cruise all perturbations are sufficiently small, we consider both the linear aerodynamics and the equations of motion. In addition, the analysis will be confined to the pure heave motions of the vehicle under the action of the wave-induced lift.[36] In dimensional form, the instantaneous vertical posi­tion of the vehicle’s center of gravity is described by the following ordinary differential equation

A2nj N

(М + А22)-^£ = ;Г>Уп, (7.40)

71— 1

where M and Л22 are the mass and added mass of the vehicle, the latter corresponding to the inertial force in the direction of у axis in motion along the same axis, T~Lcg represents a dimensional distance of the center of gravity from the unperturbed ground surface, and T is dimensional time. The right – hand side of equation (7.40) contains external aerodynamic forces, acting in the vertical direction. We render (7.40) nondimensional, using the root chord C0 and the cruise speed U0 of the vehicle as characteristic quantities. Substituting the nondimensional parameters in (7.40), we obtain

In (7.41), СУп is the contribution of the lift force RVn to the total lift coeffi­cient, S stands for the reference area of the wing, and p is the density of the air. Neglecting the added mass Л22 with respect to the mass of the vehicle, we obtain the following nondimensional equation:

A2u n

= <[37]-42>

П— 1

where /X = 2M/pSC0 is the doubled relative density of the vehicle based on the reference volume VT = SC0. Introducing the perturbation of the ground clearance h(t) = hcg — /г, where h is the time-averaged relative ground clear­ance, we rewrite (7.42) as

j2 I N

^ = ЕС».- <7-43>

n—1

We represent the right-hand side of (7.43) as the sum of three lift coefficients responsible for contributions of the aerodynamic action of the waves and the heave response of the vehicle,

Cy(t) = Cyjt) + ~^h{t) + CVh(t), (7.44)

where CVw is the wave-induced lift coefficient, and the second term represents the “spring” feature of the dynamic air cushion under the lifting surface in cruise, i. e., the response of the vehicle to the perturbation of the ground clearance.[38] The last term is due to the wave-induced heave rate and the ac­celeration. By using the results obtained in paragraphs 3.6 and 7.1, dedicated correspondingly to heave oscillations and the motion of a wing above wavy ground, we can write formula (7.44) in more detail:

Cy(t) = <^rCvl(A, к) exp(ikt) + к), (7.45)

where aw is the amplitude of the wave as a fraction of the root chord, і = л/—T, к = 27r/Lw is the Strouhal number, and Lw is the wavelength related to the root chord. In all cases we assume as meaningful only real part of the complex expressions. The parameters Cw and Сh represent the complex amplitudes of the wave-induced lift coefficient and the lift coefficient due to the heave. Assuming that the wave-induced oscillations take place for a long time so that free oscillations are damped, we restrict the analysis to “forced ” motions with the nondimensional frequency of the waves. For harmonic oscillations,

h = —k2h, so that the formula for heave motions induced by waves on the ground becomes

~ _ aw0Cw(Л, k) exp(ikt)

[ j ” h2[dCy/dh + k2n + iCh(,k)/h]

The maximum nondimensional acceleration due to heave is given by

ah = k2h(t).

Taking into account formula (3.65) for the lift coefficient Cy of a flat plate in a steady ground effect, we can derive an approximate relationship between the cruise lift coeficient and its derivative in height:

_ Cyo

dh ~ h ’

One can also link the (doubled) density (i of the vehicle and its cruise lift coefficient in the following way:

CyoFr2 = Ц,

016

2n k= —

Ц*

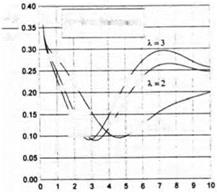
Fig. 7.17. The wave-induced heave accelerations of a rectangular wing versus the Strouhal number for different magnitudes of the aspect ratio (h = 0.2, /і — 75, Cyo = 0.65, aw = 0.03).

where Fr = UQ/y/gC0 is the Froude number based on the root chord. With this in mind, the maximum (dimensional) wave-induced heave acceleration Лъ as a fraction of the gravity acceleration g can be shown as

Ah _ Qw^|Cw(A, k)/Cw(, 0)|fc2 g ~Cyo +/i/ifc2 + iCh(A, fc)|’

In some cases it may be more convenient to use the parameters Fr and Cyo than the relative density of the vehicle fi and the lift coeffcient Cyo. In this case (7.49) can be written in the alternative form

Ah awFr2CyoCw(,k)/Cw(,0)k2 g I — Cyo + k2hFr2Cyo + іСтДА, fc)| ’ j

Figures 7.17 and 7.18 illustrate the dependence of the acceleration level on the Strouhal number (the ratio of the wavelength to the chord) for dif­ferent aspect ratios and ground clearances. In particular, Fig. 7.17 shows the behavior of the acceleration level versus the Strouhal number for different as­pect ratios of the lifting surface. Figure 7.18 demonstrates the dependence of the wave-induced heave accelerations upon the Strouhal number for different magnitudes of the relative ground clearance.

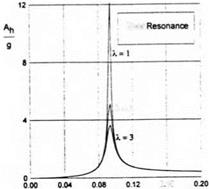
An analysis of the calculations shows that for certain combinations of the cruise lift coefhcent, the relative density of the vehicle, and the relative ground clearance, the wave-induced heave of the vehicle can become resonant. It follows from the heave equation (7.43) that nondimensional frequency (the Strouhal number) of free oscillations kf is given by

Fig. 7.18. Wave-induced heave accelerations of a rectangular wing versus the Strouhal number к for different magnitudes of the relative ground clearance (Л = 2, /X = 75, Cyo = 0.65, aw = 0.03).

or by using the relationship between dCy /dh and the lift coefficient in cruise C’yo >

When the nondimensional frequency of the forced oscillations approaches kf, the heave motion due to waves becomes resonant. For large first-generation ekranoplans the magnitudes kf are small. If, as an example, we take (i = 75, h = 0.1, and Cyo = 0.65, the resulting critical Strouhal number can be found to be 0.294 which corresponds to the ratio of the wavelength to the chord equal to 21.3. It means that for a wing chord of the order of 18 meters the resonant wavelength would be about 385 meters. Further consideration of calculated results demonstrates that with an increase in the relative density and relative ground clearance the wave-induced heave motions diminish. At the same time, increases in the wave height and the cruise lift coefficient lead to an increase in wave-induced motions.

The structure of the formula (7.49) reflects the character of the depen­dence of wave-induced heave motions on the most important design parame­ters, such as the relative density of the vehicle, the cruise lift coefficient, the aspect ratio of the main wing, the relative ground clearance, as well as upon the parameters of the waviness of the underlying surface, i. e., wavelength and amplitude.

It should be noted that heave accelerations, exemplified above, are associ­ated with flight above a solid wavy wall. When considering the corresponding effects of sea waves, we should take into account that with a decrease of the wavelength (an increase in the Strouhal number) the height of the wave dimin­ishes.[39] Therefore, the expected amplutude of the wave would be considerably smaller. It is also worth mentioning that the estimations discussed in this paragraph are very approximate and provide some qualitative information on the influence of different factors on accelerations due to the waviness of the ground.