Vortex Theory

5.1 Introduction

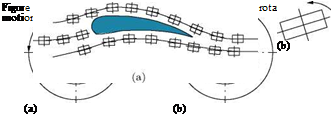
Before getting into the dynamics of vortex motion, it is essential to have a thorough understanding of rotational and irrotational flows. Translation and rotation are the two types of basic motion in a fluid flow. These two may exist independently or simultaneously. When they coexist they may be considered as one superimposed on the other. It should be emphasized that rotation refers to the orientation of a fluid element and not the path followed by the element. Thus, for an irrotational flow, if a pair of small sticks were placed on a fluid element it can be observed that the orientation is retained even while the fluid element moves along a circular path, as shown in Figure 5.1(a). In other words, in an irrotational flow, the fluid elements do not rotate about their own axes, that is, fluid elements do not spin in an irrotational flow. But in a rotational flow, fluid elements rotate about their axes, as shown in Figure 5.1(b). Thus, in an irrotational flow, like the one shown in Figure 5.1(a), the fluid elements move along circular paths but do not rotate about their own axes. Thus, the angular velocity of fluid elements in an irrotational flow is zero. If the flow field were rotating like a rigid body, then the fluid elements in the field would experience a rotation about their own axes, as shown in Figure 5.1(b). This type of motion is termed rotational and cannot be described with a velocity potential.

If the possible distortion of the fluid elements caused by severe viscous traction is ignored then there are only three possible ways in which a fluid element can move. They are the following:

(a) Pure translation – the fluid elements are free to move anywhere in space but continue to keep their axes parallel to the reference axes fixed in space, as shown in Figure 5.2(a). The flow in the potential flow zone, outside the boundary layer over an aerofoil, is substantially this type of flow.

(b) Pure rotation – the fluid elements rotate about their own axes which remain fixed in space, as shown in Figure 5.2(b).

(c) The general motion in which translation and rotation are compounded. Such a motion is found, for example, in the wake of a bluff body.

A flow in which all the fluid elements behave as in item (a) above is called potential or irrotational flow. All other flows exhibit, to a greater or lesser extent, the spinning property of some of the constituent fluid elements, and are said to posses vorticity, which is the aerodynamic term for elemental spin. The flow is then termed rotational Bow.

From the above descriptions it is evident that a flow is either rotational, possessing vorticity, or irro­tational, for which vorticity is zero. The rotational and irrotational nature and the properties of a flow

Theoretical Aerodynamics, First Edition. Ethirajan Rathakrishnan.

© 2013 John Wiley & Sons Singapore Pte. Ltd. Published 2013 by John Wiley & Sons Singapore Pte. Ltd.

Figure 5.1 (a) Irrotational flow, (b) rotational flow.

can be examined analytically, leading to the development of characteristic equations governing the flow. Using these equations, the nature of any unknown flow can be analyzed.