Circulation

Circulation is the line integral of a vector field around a closed plane curve in a flow field. By definition:

(5.3)

where Г is circulation, V is flow velocity tangential to the streamline c, encompassing the closed curve under consideration, and ds is an elemental length.

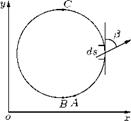
If a line AB forms a closed loop or circuit in the flow, as shown in Figure 5.4, then the line integral of Equation (5.3) taken round the circuit is defined as circulation, that is:

= I (udx + v dy),

AB

where u is the component of V is the x-direction and v is that in the y-direction. Note that the circuit is imaginary and does not influence the flow, that is, it is not a boundary. In Equation (5.3), both V and ds are vectors. Therefore, the dot product of V and ds results in above expression for Г.[2]

Circulation implies a component of rotation of flow in the system. This is not to say that there are circular streamlines, or the elements, of the fluid are actually moving around some closed loop although this is a possible flow system. Circulation in a flow means that, the flow system could be resolved into an uniform irrotational portion and a circulating portion. Figure 5.5 illustrates concept of circulation.

This implies that, if circulation is present in a fluid motion, then vorticity must be present, even though it may be confined to a restricted space, as in the case of the circular cylinder with circulation, where

Figure 5.4 A loop AB in a flow field.

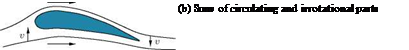Figure 5.5 Illustration of circulation.

the vorticity at the center of the cylinder may actually be excluded from the region of flow considered, namely that outside the cylinder.

An alternative equation for circulation Г can be obtained by considering the circuit of integration made up of a large number of rectangular elements of sides Sx and Sy, as shown in Figure 5.6.

Г = (udx + v dy),

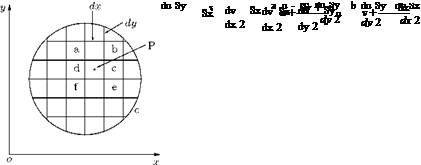Applying the integral round the element abcd with point P(x, y) at its center, where the velocity components are u and v, as shown in Figure 5.6, we get:

Simplification of this results in:

dv du

AT = dx – dy {SxSy)-

The sum of the circulations of all the elemental areas in the circuit constitutes the circulation of the circuit as a whole. As the circulation AT of each element is added to the AT of the neighboring element, the contributions of the common sides disappear. Applying this reasoning from an element to the neighboring element throughout the area, the only sides contributing to the circulation, when the ATs of all areas are summed together, are those sides which actually form the circuit itself. This means that, for the total circuit c, the circulation becomes:

— (dxdy)

= (udx + v dy)

and the vorticity Z is given by:

dv du

^ dx dy

If the strength of the circulation T remains constant whilst the circuit shrinks to encompass an elemental area, that is, until it shrinks to an area of the size of a rectangular element, then:

T = Z x (SxSy) = Z x area of element.

Therefore,

Vorticity = lim. (5.4)

area^0 area of element

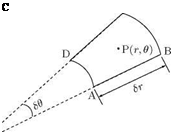
This is a result which enables an easy derivation of the vorticity relation in polar coordinates.

Let us consider a segment of a fluid element of width Sr, subtending angle SO, at the origin and width Sr, as shown in Figure 5.7. If the segment is located at the point P(r, O), where the normal and tangential

axis

Figure 5.8 (a) Straight line vortex, (b) cross-section showing the associated streamlines.