Laws of Vortex Motion

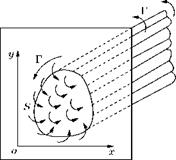
In Section 5.4, we saw that a point vortex can be considered as a string of rotating particles surrounded by fluid at large moving irrotationally. Further, the flow investigation was confined to a plane section normal to the length or axis of the vortex. A more general definition is that a vortex is a Bow system in which a finite area in a plane normal to the axis of a vortex contains vorticity. Figure 5.10 shows a sectional area S in the plane normal to the axis of a vortex. The axis of the vortex is clearly, always normal to the two-dimensional flow plane considered and the influence of the so-called line vortex is the influence, in a section plane, of an infinitely long straight line vortex of vanishingly small area.

The axis of a vortex, in general, is a curve in space, and area S is a finite size. It is convenient to consider that the area S is made up of several elemental areas. In other words, a vortex consists of a bundle of elemental vortex lines or filaments. Such a bundle is termed a vortex tube, being a tube bounded by vortex filaments.

The vortex axis is a curve winding about within the fluid. Therefore, it can flexure and influence the flow as a whole. The estimation of its influence on the fluid at large is somewhat complex. In our discussions here the vortices considered are fixed relative to some axes in the system or free to move in a controlled manner and can be assumed to be linear. Furthermore, the vortices will not be of infinite length, therefore, the three-dimensional or end influence must be accounted for.

In spite of the above simplifications, the vortices conform to laws of motion appropriate to their behavior. A rigorous treatment of the vortices, without the simplifications imposed in our treatment here can be found in Milne-Thomson (1952) [2] and Lamb (1932) [3].