Vortex Theorems

Now let us have a closer look at the theorems governing vortex motion. Consider the circulation of a closed material line. By definition (Equation 5.3), we have the circulation as:

The time rate of change of Г can be expressed as:

(5.7)

since ds/dt = V, where V is the velocity, s is length and t is time. The second integral in Equation (5.7) vanishes, since V ■ dV = d ^V ■ is the total differential of a single valued function, and the starting point of integration coincides with the end point.

By Euler equation, we have:

where FB is the body force. From Equation (5.7) and the Euler equation, we obtain the rate of change of the line integral over the velocity vector in the form:

(5.8)

In Equation (5.8), Dr/Dt vanishes if (FB ■ ds) and yр/р can be written as total differentials. When the body force FB has a potential (that is, when the body force is a conservative force field); implying that the work done by the weight in taking a body from a point P to another point Q is independent of the path taken from P to Q, and depends only on the potential, the first closed integral in Equation (5.8) becomes zero because:

FB ■ ds =— y ф ■ ds =— d^.

For a homogeneous density field or in barotropic flow, the density depends only on pressure, that is р = f (p). For such a flow, the second term on the right-hand side of Equation (5.8), can be expressed as:

Therefore, for barotropic fluids, the second integral also vanishes in Equation (5.8).

Equations (5.8) to (5.10) form the content of Thompson’s vortex theorem or Kelvin’s circulation theorem. This theorem states that:

“in a Bow of inviscid and barotropic fluid, with conservative body forces, the circulation around a closed curve (material line) moving with the fluid remains constant with time, " if the motion is observed from a nonrotating frame.

The vortex theorem can be interpreted as follows:

“The position of a curve c in a flow field, at any instant of time, can be located by following the motion of all the fluid elements on the curve. "

That is, Kelvin’s circulation theorem states that, the circulation around the curve c at the two locations is the same. In other words:

where D/Dt(= d/dt + V • has been used to emphasize that the circulation is calculated around a material contour moving with the fluid.

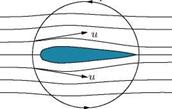
With Kelvin’s theorem as the starting point, we can explain the famous Helmholtz’s vortex theorem, which allows a vivid interpretation of vortex motions which are of fundamental importance in aerody­namics. Before venturing to explain Helmholtz’s vortex theorems, it would be beneficial if we consider the origin of the circulation around an aerofoil, in a two-dimensional potential flow, because Kelvin’s theorem seems to contradict the formulation of this circulation.

It is well known that, the force on an aerofoil in a two-dimensional potential flow is proportional to the circulation. Also, the lift, namely the force perpendicular to the undisturbed incident flow direction, experienced by the aerofoil is directly proportional to the circulation, T, around the aerofoil. The lift per unit span of an aerofoil can be expressed as:

where p and V, respectively, are the density and velocity of the freestream flow.

Now let us examine the flow around a symmetrical and an unsymmetrical aerofoil in identical flow fields, as shown in Figure 5.12. As seen from Figure 5.12(a), the flow around the symmetrical aerofoil at zero angle of incidence is also symmetric. Therefore, there is no net force perpendicular to the incident

(a)

Figure 5.12 (a) Symmetrical and (b) unsymmetrical aerofoil in uniform flow.

A A’

Figure 5.13 Velocity on either side of separation surface behind the aerofoil.

flow direction. The contribution of the line integral of velocity about the upper-half of the aerofoil to the circulation has exactly the same magnitude as the contribution of the line integral of velocity about the lower-half, but with opposite sign. Therefore, the total circulation around the symmetric aerofoil is zero.

The flow around the unsymmetrical aerofoil, as shown in Figure 5.12(b), is asymmetric. The contribu­tion of the line integral of velocity about upper-half of the aerofoil has an absolute value larger than that of the contribution about the lower-half. Therefore, the circulation around the unsymmetrical aerofoil is nonzero. By Bernoulli theorem it can be inferred that the velocity along a streamline which runs along the upper-side of the aerofoil is larger on the whole than the velocity on the lower-side. Therefore, the pressure on the upper side is less than the pressure on the lower side. Thus there is a net upward force acting on the aerofoil.

For an unsymmetrical aerofoil the flow velocity over the upper and lower surfaces are different even when it is at zero angle of incidence to the freestream flow. Because of this the pressure on either side of the dividing streamline, shown in Figure 5.13, are different. Also, the velocities on either side of the separation surface are different, as shown in the figure. This implies that the pressure on either side of the separation surface are different. It is well known that the separation surface, which is also called slipstream, cannot be stable when the pressures on either side are different [4]. The slipstream will assume a shape in such a manner to have equal pressure on either side of it. Here the pressure at the lower side is higher than that at the upper side. Thus, the slipstream bends up, as shown in Figure 5.14(a).

At the first instant of start-up, the flow around the trailing edge of the aerofoil is at very high velocities. Also, the flow becomes separated from the upper surface. Flow field around an aerofoil at different phases of start-up is shown in Figure 5.14. The separation at the upper surface is caused by the very large deceleration of the flow from the maximum thickness location to the separation point S, which is formed

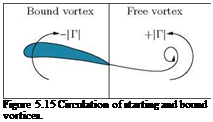on the upper surface since the flow is still circulation-free flow [Figure 5.14(a)]. This flow separates from the upper surface even with very little viscosity (that is, g ^ 0) and forms the wake, which becomes the discontinuity surface in the limiting case of g = 0. The flow is irrotational everywhere except the wake region. Soon after start-up, the separation point is dipped to the trailing edge, as per Kutta hypothesis, and the slipstream rolls-up as shown in Figure 5.14(b). The vortex thus formed is pushed downstream and positioned at a location behind the aerofoil, as shown in Figure 5.14(c). This vortex is called starting vortex. The starting vortex is essentially a free vortex because it is formed by the kinematics of the flow and not by the viscous effect.

By Kelvin’s circulation theorem, a closed curve which surrounds the aerofoil and the vortex still has zero circulation. In other words, the circulation of the starting vortex and the bound vortex (this is due to the boundary layer at the surface of the aerofoil in viscous flow) are of equal magnitude, as shown in Figure 5.15.

A closed line which surrounds only the vortex has a fixed circulation and must necessarily cross the discontinuity surface. Therefore, Kelvin’s circulation theorem does not hold for this line. A curve which surrounds the aerofoil only has the same circulation as the free vortex, but with opposite sign, and therefore the aerofoil experiences a lift. The circulation about the aerofoil with a vortex lying over the aerofoil, due to the boundary layer at the surface, is called the bound vortex.

In the above discussion, we used the obvious law that the circulation of a closed loop is equal to the sum of the circulation of the meshed network bounded by the curve, as shown in Figure 5.16.

Tclosed loop ^ ‘ Гі (5Л2)

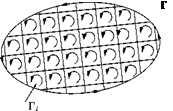That is, the sum of the circulations of all the areas is the neighboring circulation of the circuit as a whole. This is because, as the АГ of each element is added to the АГ of the neighboring element, the contribution of the common sides (Figure 5.16) disappears. Applying this argument from one element to the neighboring element throughout the area, the only sides contributing to the circulation when the Ars of all elemental areas are summed together are those sides which actually form the circuit itself.

This means, that for the circuit as a whole, the circulation is:

In this relation, the surface integral implies that the integration is over the area of the meshed network, and the cyclic integral implies that the integration is around the circuit of the meshed network.

For discussing the physics of Helmholtz’s theorem, we need to make use of Stoke’s integral theorem.