Shock – sonic surface interaction in 3D flow

Compared to the rich variety of analytical models in plane transonic flow, our knowledge of local transonic phenomena in three-dimensional flow is much more limited. Equations (64H67) allow a construction of axisymmetric near sonic flow models, but the system is stilt weakly nonlinear so that basic solutions (781 may not be superimposed. Fully 3D flow docs not permit a hodo – graph-type mapping, our knowledge base is restricted to experiments and evaluation of refined numerical analysis results. For design, a detailed knowledge base is needed to prepare a physi­cally consistent and mathematically well-posed input for a reasonable numerical simulation. In­verse design methods arc aimed at finding configurations with prescribed pressure distributions. This is a very attractive approach for practical design but inconsistencies between geometrical constraints and desired flow quality may occur: Ideal design goals may ignore the fact that una­voidable shock waves will accompany the envisioned flow patterns.

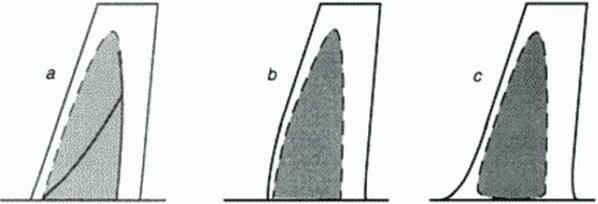
An example is the design of a swept transonic w ing fixed to a wall or a fuselage w ith­out any fillet: the non-orthogonal comer angles between wing and sidewall do not allow for a smooth pressure distribution in the sonic expansion and rccompression domain. Oblique shocks fonn and travel into the spanwise direction, eventually coalescing to stronger rccompression waves, see Figure 37a Only a locally unswept surface geometry can accomodate smooth expan­sion and rccompression across sonic flow conditions (Figure 37b). Another way to avoid this purely inviscid feature of the flow – and at the same time also influence viscous flow interaction favorably is the design of a fillet (Figure 37c) which provides a smooth surface without comers at the wing root. This qualitative sketch of 3D flow features is based on practical designers’ experience, supported by an extrapolation of the well-developed knowledge base for 2D flows.