Gasdynamic manipulations for design purposes
The basic differential equations for compressible flow to be solved with numerical methods for practically interesting aerodynamic applications are the Reynolds-averaged Navier-Stokes equations Neglecting viscous effects reduces this system of equations to the Euler equations. Gasdy – namic phenomena such as shock waves in a flow field arc simulated with sufficient accuracy by numerical algorithms for the latter inviscid model equations. Consequently, an inviscid flow design approach makes use of the Euler equations in suitable ways to help finding flows with reduced or vanishing shock waves. Techniques developed for shock wave control arc then implemented successfully also in the Navier-Stokes equations. In this paragraph, a special approach to control shock wave strength is outlined: Tlie Fictitious Gas (FG) method. This method was already developed when numerical algorithms to solve the compressible potential flow differential equations resulted in the first applied aerodynamic analysis computer programs (89). In the meantime, the increased requirements for higher aerodynamic efficiency of an aircraft seems to justify a rev iew of the theoretical ptytential of the FG method. In the following, first the purely "fictitious” part, i. c. the abstract mathematical model for the method is explained with the atm of a practical application. Second, the most recent results of classical shock-free flow construction by the FG method is illustrated and third, practical methods for rapid aerodynamic design derived from these approaches, using both the knowledge base for phenomena modelling and proven CFD axles is outlined.
|
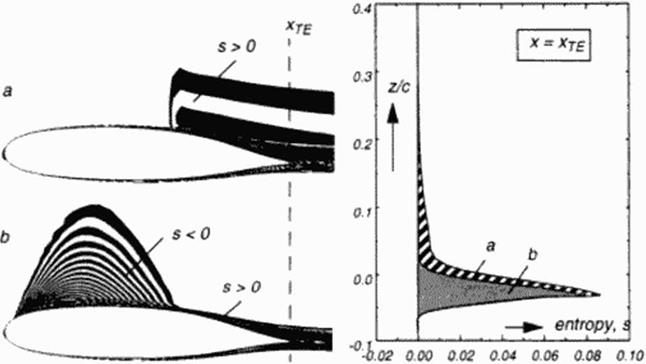
Figure 41 Comparison of viscous transonic flow (M„ • 0.7, Re = 20 Mill., c, = 0.6) past u given airfoil without (above, a) and with (below, b) flow control, carried out by energy removal within the supercritical domain. Entropy level isofringes and wake profile at the trailing edge indicate drug reduction of 35%. |