Forced Vortex

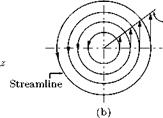
Forced vortex is a rotational flow field in which the fluid rotates as a solid body with a constant angular velocity ю, and the streamlines form a set of concentric circles. Because the fluid in a forced vortex rotates like a rigid body, the forced vortex is also called Bywheel vortex. The change of total energy per unit weight in a vortex motion is governed by Equation (5.65).

The velocity at any radius r is given by:

 

V = юг

 

From this we have:

 

and

 

V — = ю. r

 

Substituting dV/dr and V/r into Equation (5.65), we get:

 

dH юг — = —(ю + ю) dr g

 

2ю2г g ‘

 

Integrating this we get:

 

(5.66)

 

H = ——- + с, g

 

where с is a constant. By Bernoulli equation, at any point in the fluid, we have:

 

p V2 H =——– + T)—+ z. pg 2g

 

Axis of rotation Free surface

Velocity variation V ~ r

Figure 5.37 Forced vortex (a) shape of free surface, (b) velocity variation.

Note that, in the above equation and Equation (5.66), the unit of the total head is meters. Substitution of this into Equation (5.66) results in:

P	-2r2		-2r2
	+— “—	+ z =	z —–	+ c
Pg	2g		g
	P		– 2 r2
		+ z =		+ c.
	Pg		2g

If the rotating fluid has a free surface, the pressure at the surface will be atmospheric; therefore, the pressure at the free-surface will be zero.

P

Replacing — with 0 in the above equation, the profile of the free surface is obtained as:

Pg

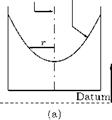
Thus, the free surface of a forced vortex is in the form of a paraboloid.

Similarly, for any horizontal plane, for which z will be constant, the pressure distribution will be given by:

22

– = – rj – + (c – z). (5.68)

Pg 2g

The typical shape of the free surface and the velocity variation along a radial direction of a forced vortex are shown in Figure 5.37.