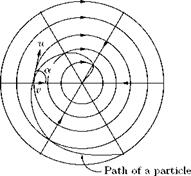
Free Spiral Vortex

A free spiral vortex is essentially the combination of a free cylindrical vortex and a radial flow. Before getting into the physics of free spiral vortex, let us see what is a radial flow.

Radial Flow

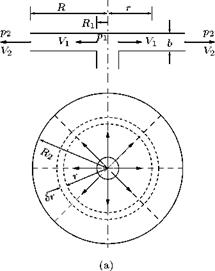
Examine the flow between two parallel planes as shown in Figure 5.40. In the flow the streamlines will be radial straight lines and the streamtube will be in the form of sectors. This kind of flow in which the fluid flows radially inwards, or outwards from a center is called a radial flow. The area of the flow will therefore increase as the radius increases, causing the velocity to decrease. The flow pattern is symmetrical and therefore, the total energy per unit weight H will be the same for all streamlines and for all points along each streamline if we assume that there is no loss of energy.

If Vr is the radial velocity and p is the pressure at any radius r, then the total energy per unit weight H becomes:

p V2

H =——— 1— = constant. (5.72)

Pg 2g

Assuming the flow to be incompressible (as would be the case of a liquid), by continuity, we have the volume flow rate Q as:

Q = area x velocity
= 2nrb x Vr,

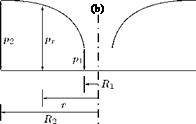Figure 5.40 A radial flow: (a) streamlines, (b) pressure variation.

where b is the distance between the planes. Thus,

Substituting this into Equation (5.72), we get:

If the radial flow discharges to atmosphere at the periphery, the pressure at any point between the two plates will be below atmospheric (that is, subatmospheric); there will be a force tending to bring the plates together and so shut-off the flow. This phenomenon can be observed in the case of a disc valve. Radial flow under the disc will cause the disc to be drawn onto the valve seating. This will return to atmospheric and the static pressure of the fluid on the upstream side of the disc will push it off its seating again. The disc will tend to vibrate on the seating and the flow will be intermittent.

Now, let us find an expression for the pressure difference between two points on the same horizontal plane in a free vortex. For a free cylindrical vortex, the streamlines are concentric circles and there is no variation of the total energy with radius, that is:

— = 0.

dr

Also, by Equation (5.69), we have:

Let p1 and p2 be the pressures in two concentric streamlines of radii r1 and r2 which have velocities V1 and V2, respectively. Since there is no change of total energy with radius, for the same horizontal plane, by Bernoulli equation:

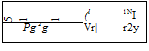(5.74)

Now, let us obtain an expression for the pressure difference between two points at radii R1 and R2 ,ona radial line, when a fluid flows radially inward or outward from a center, neglecting friction. Flow is radial and therefore in straight line so that r, the radius of curvature of the streamlines, is infinite, dH/dr = 0, and for all streamlines:

p V2

H =——- 1—– = constant.

Pg 2g

If p1 and p2 are the pressures at radii R1 and R2, respectively, where the velocities are V1 and V2:

P1 – P2 V| – V2

Pg 2g ‘

By volume conservation:

Figure 5.41 A free spiral vortex.

It is evident from Equations (5.73) and (5.74) that the relation between pressure and radius and between velocity and radius is similar for both free vortex and radial flow. Both types of motion may therefore occur together. The fluid rotates and flows radially forming a free spiral vortex in which a fluid element will follow a spiral path, as shown in Figure 5.41.