Free Vortex

Free vortex is an irrotational flow field in which the streamlines are concentric circles, but the variation of velocity with radius is such that there is no change of total energy per unit weight with radius, so that dH/dr = 0. Since the flow field is potential, the free vortex is also called potential vortex.

For a free vortex, from Equation (5.65), we have:

	0=	V
dV	dr	g
—	+ — =	0.
V	r

V dV ~ + ~dr

or

Vr = c,

where c is a constant known as the strength of the vortex at any radius r. The tangential velocity becomes:

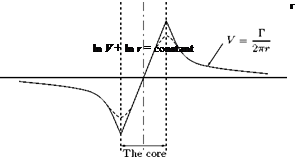
This shows that in the flow around a vortex core the velocity is inversely proportional to the radius (see Section 5.4). When the core is small, or assumed concentrated on a line axis, it is apparent from the relation V = c/r that when r is small V can be very large. However, within the core the fluid behaves as though it were a solid cylinder and rotates at an uniform angular velocity. Figure 5.38 shows the variation of velocity with radius for a typical free vortex. The solid line represents the idealized case, but in reality it is not so precise, and the velocity peak is rounded off, as shown by the dashed lines.

At any point in the flow field, by Bernoulli equation, we have:

V2

+ ^ + г = H. 2g

Substituting Equation (5.69), we get:

P c2

—— + 9- 2 + г = H

Pg 2gr2

At the free surface, — = 0. Thus, the profile of the free surface is given by:

Pg

This is a hyperbola asymptotic to the axis of rotation and to the horizontal plane through г = H, as shown in Figure 5.39.

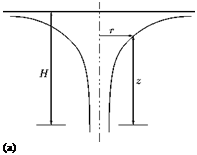Figure 5.39 Free vortex: (a) shape of free surface, (b) velocity variation.

For any horizontal plane, z is constant and the pressure variation is given by:

Thus, in a free vortex, pressure decreases and circumferential velocity increases as we move towards the center, as shown in Figure 5.39.

The free vortex discussed above is essentially a free cylindrical vortex. The fluid moves along stream­lines that are horizontal concentric circles; there is no variation of total energy with radius. Combination of a free cylindrical vortex and radial flow will result in a free spiral vortex.