Physical Meaning of Circulation
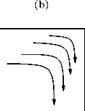
In Equation (5.3) the vector field is taken as velocity V. But the vector field need not be the flow velocity alone. The vector field can be force, mass Bow rate of a fluid, etc. Therefore, in general, the circulation may be defined as the line integral of a vector field around a closed plane curve in a flow field. If the vector is a force F, then the integral § F ■ ds is equal to the work done by the force. Taking the vector as pV, the mass flow rate per unit area, we can get a physical meaning of the circulation in the following way. Imagine a tiny paddle-wheel probe is placed [Figure 5.43(c)] in any of the flow patterns shown in Figure 5.43.
When the flow velocity on one side is greater than the other side, as in Figure 5.43(c), the wheel will turn. If the mass flow rate per unit area pV is larger on one side of the wheel than the other, then the circulation is different from zero, but if pV is the same on both sides as in Figure 5.43(b), then the circulation is zero. We shall show that the component of curl m along the axis of the paddle wheel equals:
lim — ® m ■ ds, (5.77)
dA^0 dA I
 |
 |
(c) (d)
Figure 5.43 Streamlines in: (a) a vortex, (b) parallel flow with constant velocity, (c) parallel flow with variable velocity, (d) flow around a corner.
where dA is the area enclosed by the curve along which we calculate circulation. The paddle wheel then acts as a “curl meter” to measure curl гіг; when the wheel does not rotate, curl гіг = 0. In Figure 5.43(c), curl гіг = 0 in spite of the fact that the streamlines are parallel. In Figure 5.43(d), it is possible to have curl m = 0 even though the streamlines go around a corner. In fact, for the flow of water around a corner curl гіг = 0. We must realize that the value of curl m at a point depends upon the circulation in the neighborhood of the point and not on the overall flow pattern.
Example 5.2
A cylindrical tank of 1 m diameter and 0.75 m height is filled with a liquid of relative density 0.9 up to 0.5 m from the bottom of the tank and the rest of the tank contains atmospheric air. The tank revolves about its vertical axis at a speed such that the liquid begins to uncover the base. (a) Calculate the speed of rotation and (b) the upward force on the cover.
Solution
The flow field described is shown in Figure 5.44.
(a) When the tank is static, the volume of oil is:
nR2zi.
While rotating, a forced vortex is formed and the free surface will be a paraboloid CGD.
Volume of oil = Volume of cylinder ABFE — Volume of paraboloid CGD = nR2z — 2 nrz.
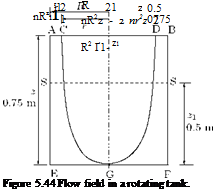 |
Since the volume of the paraboloid is equal to half the volume of the circumscribing cylinder, no oil is spilled out from the cylinder, therefore:
Show that a free vortex is an irrotational motion. A hollow cylinder of diameter 1 m, open at the top, spins about its axis which is vertical, thus generating a forced vortex motion of the liquid contained in it. Calculate the height of the vessel so that the liquid just reaches the top when the minimum depth of the free surface of the liquid (from the top) is 25 cm at 200 rpm.
Solution
The tangential velocity in a free vortex (excluding the core) is given by Equation (5.69) is:
Ve = ~,
r
where c is a constant. This field is potential if the vorticity content in the field is zero. The vorticity Z in polar coordinates is [Equation (5.2)]:
Е л. dh _ f din
r dr r Э6
In free vortex, the normal component of velocity qn = 0. Thus:
it dqt
r dr
We know that:
it_ w _c2
r r r2
and
dqt d Ґ c _ c
dr dr r) r2











