Mutual action of Two Vortices

Consider two vortices of strength у and y’ located at (0, 0) and (0, h), as shown in Figure 5.56. These two vortices repel one another if у and y’ have the same sign, and attract if the signs are opposite. This result has its application to the action between the vortices shed by the wings of a biplane.

5.19 Energy due to a Pair of Vortices

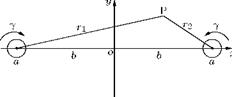
Consider two circular vortices of equal radius a and equal strength у placed as shown in Figure 5.57 with the distance 2b between their centers very large compared to a, so that their circular form is preserved.

l/h

h

Y /h

Figure 5.56 Two vortices at a finite distance between them.

Figure 5.57 Two small circular vortices at a finite distance apart.

Neglecting the interaction between them, we can write the vorticity as:

Z = iy ln (z — b) — iy ln (z + b)

The stream function is:

ф = у ln (—

Г2

where ri, r2 are the distance of the point z from the vortices, as shown in Figure 5.57. For the region external to the vortices the kinetic energy of the fluid is:

KEo = — p I I (u2 + v2) dxdy.

Now in terms of stream function ф:

2 2 дф дф

u2 + v = u——— v —

dy dx

д(иф) д(vф) du dv

ду дх ду дх

д^ф) дфф) (дv дu

ду дх + ^ 1 дх ду

But the region outside the vortices is irrotational and hence vorticity:

дv дu ^ дх ду

Thus,

Therefore, we have:

д(uф) ду	д(vф) дх
1 KEo = — p o 2
dxdy.

By Stokes theorem:
d(u^) dy	д(уф) dx
dxdy = — uф dx + уф dy.
Thus:

1

KE0 = 2 p x 2
(цф dx + уф dy).

The integration is taken positively (in the counterclockwise direction) round c, and the circumference of the vortex at z = b. The factor 2 is to account for the two vortices contributing the same amount to the energy.

Now:

u dx + vdy = Vsds,

where Vs is the speed tangential to contour c and ds is arc length along c. Therefore:

Vs ds = 2ny the circulation.

Also, on c, r1 = a, and r2 = 2b (approximately), so that we may express the KE0 as:

KEo = – p x 2ny x у ln (2b)

= 2npyL ln — .

a

The fluid inside the contour c is rotating (Figure 5.48) with angular velocity у/a[6] 2 and moving as a whole with velocity y/2b induced by the other vortex. Thus the KE inside c is:

2 / 1 y[7] 1 a2 у2

KEi = nap 24b2 + 2 x 2 a4l ‘

where the first term is the contribution due to the whole motion and the second term is due to the angular velocity (r«). But a2/b2 is small and hence can be neglected. Hence: