Osculating Cones (OC) Waveriders
8.3.1 Generalization of the conical flow w a vender
Л suitable selection of strcamsurfaccs from a given analytical or numerical solution for a 3D supersonic flow with a shock system may define the solid boundary of an obstacle in this flow, with the shock waves mthe flow generated by this obstacle. This is the basic design principle of the waverider, which is basically a simple supersonic generic aircraft. Renewed interest in high Mach number supersonic and hypertonic transport vehicle design revived the classical wavender principle using wedge and cone flows to carve out a multiplicity of shapes, suitably parameterized and shapes selected by optimization strategies (102). This is made possible in a fast and efficient way because the used flow solution is known and so arc pressures along the contour, integrated to lift and drag at inviscid flow design conditions very’ easily. Furthermore, known streamlines allow for a quasi – 2D boundary layer computation, subsequent shape correction and viscous drag computation. Viscous flow optimized waveriders are therefore the starting point to a refined configuration definition for high speed transport aircraft
Combining plane and axisymmetric flow: Slope surface shock waves
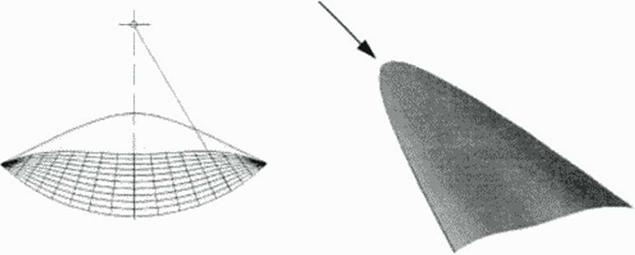
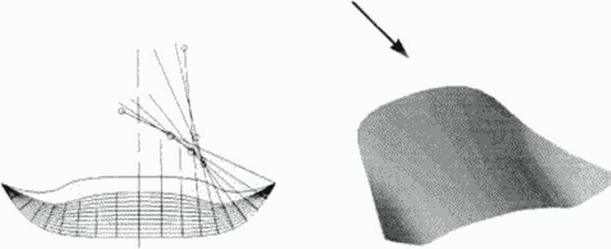
Wavender aircraft have supersonic leading edges of a completely integrated wing • body configuration. Planar 2D flows arc suitable for lifting w ings with sufficient span but suffer from low volumetric efficiency. Conical flows give better volume but have a small aspect ratio resulting in bad low speed performance. A compromise is a higher order approximation to exact model flows by a spanwise van at ion of the local cone radius it is an application of the above
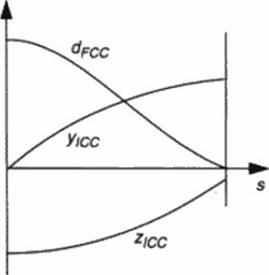
mentioned validity of locally axi symmetric flow. Figure 49 illustrates the geometric definition of a conical or generalized shock segment bounded by the waverider inlet capture curve (ICC) coordinates and the leading edge which serves as a flow capture curve (FCC). This definition of a shock wave patch with given obliquity angle P includes planar, conical and slope surface shock waves with constant strength. The latter are envelopes of a single cone sliding along the given leading edge (FCC) in 3D space, and the idea to approximate the resulting flow field behind such shock waves by the local tangent cone flow meridional (osculating) plane results in relatively high accuracy of this straightforward definition of the lower surface along with us pressure distribution.
As in previous waverider work, the upper surface may be a free stream surface or has to be designed for additional lift by convex contouring for flow expansion. In the following illustrations some examples designed with software based in this principle is shown. Fast design codes based on this method have been developed by various authors. Extensions fix refined viscous flow modelling and for incorporating propulsive devices have been developed.
 |
 |
N
Figure 49 Defining the bow wave of a conical flow* waverider: Inlet capture curve (ICC) and leading edge or flow capture curve (FCC). Generalization* for OC waverider* if ICC is not a circle, shock segment is a slope surface, shock angle is P
|
|
|
Figure 50 Waveridere generated from bow shocks (shock angle (5 ■ 18°) in supersonic freestream of M. * 4. Cone-derived (above) and OC configuration |