Vortex between Parallel Plates

Let us consider a vortex of strength y midway between the planes y = ±a/2 and at the origin, as shown in Figure 5.53.

The transformation Z = ienz/a would map the strip between the planes on the upper half of the f-plane (the thick and thin lines in Figures 5.53(a) and 5.53(b) indicate which parts of the boundaries correspond) as follows:

The streamlines of a vortex at the origin between two parallel plates would be as shown in Figure 5.54.

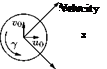
Figure 5.55 Circular vortex in a flow field.

Note that the walls increase the velocity component u when x = 0 and decrease v when у = 0.In other words, the walls make the vortex to stretch along the x-direction and shrink along the у-direction.

5.18 Force on a Vortex

A rectilinear vortex may be regarded as the limit of a circular vortex which rotates about its center as if rigid. Consider a circular vortex inserted in a steady flow field as shown in Figure 5.55, so that its center is at the point whose velocity is (u0, v0) before the vortex is inserted. The vortex would then move with the fluid with velocity (u0, v0) soon after inserting, so that the flow motion would no longer be steady. Let us imagine the vortex to be held fixed by the application of a suitable force (in the form of pressure distribution). This force would be equal but opposite to that exerted by the fluid on the vortex.

When the motion is steady, the force exerted by the fluid is the Kutta-Joukowski lift which is indepen­dent of the size and shape of the vortex. This force, being independent of the size, is also the force exerted by the fluid on a point vortex. The direction of the force (shown in Figure 5.55) is obtained by rotating the velocity vector through a right angle in the direction opposite to that of the circulation (vorticity).