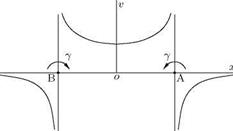
Vortex Pair

Two vortices of equal strength у but opposite nature (one rotating clockwise and the other rotating counterclockwise) from a vortex pair, as shown in Figure 5.51.

Each vortex in the pair induces a velocity y/AB on the other, in the direction perpendicular to AB and in the same sense. Thus the vortex pair moves in the direction perpendicular to AB, remaining at the constant distance AB apart. The fluid velocity at O, the mid-point of AB, is:

2y 2Y 4Y AB + AB = AB’

which is four times the velocity of each vortex (see Figure 5.49).

Taking O as the origin and the x-axis along OA, if AB = 2a, we have the complex potential, at the instant when the vortices are on the x-axis, as:

w = iY ln (z — a) — iY ln (z + a). (5.78)

Thus,

• ■ 1 1

u — iv = iy —

z — a z + a

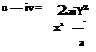With y = 0, this gives the velocity distribution along the x-axis as:

Thus u = 0, v = — 2aY/(x2 — a2). The plot of v against x is shown in Figure 5.52.

The curve is as per the equation v(x2 — a2) = —2aY, so that the asymptotes are the straight portions of Figure 5.52 go over into the asymptotes x ± a and thus the velocity of vortex A cannot be reached in Figure 5.52, although this is still one-quarter of the velocity at O.

5.17 Image of a Vortex in a Plane

For a vortex shown in Figure 5.51, because of symmetry there will not be any flux across yy’, the perpendicular bisector of AB. Thus yy’ can be regarded as a streamline and could therefore be replaced by a rigid boundary. Hence the motion due to a vortex at A in the presence of this boundary is the same as the motion that would result if the boundary were removed and an equal vortex of opposite rotation were placed at B. The vortex at B is called the image of the actual vortex at A with respect to the plane boundary and the complex potential is still given by Equation (5.78).