Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Comparison with flight
Table 4.8 presents a comparison of the stability characteristics of Puma and Bo105 Helisim with flight estimates derived from the work of AGARD WG18 (Refs 4.22, 4.23). Generally speaking, the comparison of modal frequencies is very good, while dampings are less well predicted, particularly for the weakly damped or unstable phugoid and spiral modes. The pitch/heave subsidences for the Bo105 show remarkable agreement while the roll subsidence appears to be overpredicted by theory, although this is largely attributed to the compensating effect of an added time delay in the adopted model structure used to derive the flight estimates (Ref. 4.22). This aspect is returned to in Chapter 5 when results are
|
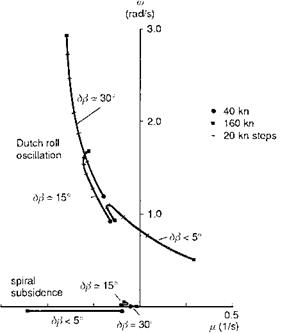
Fig. 4.29 Loci of Dutch roll and spiral mode eigenvalues with speed for different sideslip perturbations for Puma |
|
Table 4.8 Comparison of flight estimates and theoretical predictions of Puma and Bo105 stability characteristics
|
Shorthand notation:
X Complex variation ^ ± i&>;
[Z, o)n] damping ratio and natural frequency associated with roots of X2 + 2f&>„X + a>n2; (1/r) inverse of time constant т in root (X — 1 /т);
+Puma flight estimates from Glasgow/DRA analysis in Ref. 4.22;
++Bo105 flight estimates from DLR analysis in Ref. 4.22.
presented from the different model structures used for modelling roll response to lateral cyclic.
The above discussions have concentrated on 6 DoF motion analysis. There are several areas in helicopter flight dynamics where important effects are missed by folding the rotor dynamics and other higher order effects into the fuselage motions in quasi-steady form. These will be addressed in the context of constrained stability and aircraft response analysis in Chapter 5.
