Exercise Problems

1. Evaluate the vorticity of the following two-dimensional flow.

(i) u = 2xy, v = x2.

(ii) u = x2, v = —2xy.

(iii) ur = 0, Ug = r.

(iv) Ur = 0, Ug = 1.

[Answer: (i) 0, (ii) —2(x + y), (iii) 2, (iv) 0]

2. If the velocity induced by a rectilinear vortex filament of length 2 m, at a point equidistant from the extremities of the filament and 0.4 m above the filament is 2 m/s, determine the circulation around the vortex filament.

[Answer: 5.414 m2/s]

3. A point P in the plane of a horseshoe vortex is between the arms and equidistant from all the filaments. Prove that the induced velocity at P is:

Г(1 + V2)

v =————– ,

nAB

where Г is the intensity and AB is the length of the finite side of the horseshoe.

Ш Figure 5.59 A sprinkler.

4. If the velocity induced by an infinite line vortex of intensity 100 m2/s, at a point above the vortex is 40 m/s, determine the height of the point above the vortex line.

[Answer: 0.398 m]

5. If a wing of span 18 m has a constant circulation of 150 m2/s around it while flying at 400 km/h, at sea level, determine the lift generated by the wing.

[Answer: 367.5 kN]

6. If the tangential velocity at a point at radial distance of 1.5 m from the center of a circular vortex is 35 m/s, determine (a) the intensity of the vortex and (b) the potential function of the vortex flow.

[Answer: (a) 329.87 m2/s, (b) 52.5 9]

7. Show that a circular vortex ring of intensity Г induces an axial velocity 2R at the center of the ring, where R is the radius of the vortex.

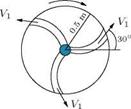
8. A rotating device to sprinkle water is shown in Figure 5.59. Water enters the rotating device at the center at a rate of 0.03 m3/s and then it is directed radially through three identical channels of exit area 0.005 m2 each, perpendicular to the direction of flow relative to the device. The water leaves at an angle of 30° relative to the device as measured from the radial direction, as shown. If the device rotates clock wise with a speed of 20 radians/s relative to the ground. Compute the magnitude of the average velocity of the fluid leaving the vane as seen from the ground.

[Answer: 9.16 m/s, at an angle of 79° with respect to the ground (horizontal)]

9. Determine an expression for the vorticity of the flow field described by:

V = x2yi — xy2 j.

Is the flow irrotational?

[Answer: Z = Zzk = — (x2 + y2) k. The flow is not irrotational, since the vorticity is not zero.]

10. When a circulation of strength Г is imposed on a circular cylinder placed in an uniform incompressible flow of velocity Ux, the cylinder experiences lift. If the lift coefficient CL = 2, calculate the peak (negative) pressure coefficient on the cylinder.

[Answer: — 4.373]

11. A wing with an elliptical planform and an elliptical lift distribution has aspect ratio 6 and span of 12 m. The wing loading is 900 N/m2, when flying at a speed of 150 km/hr at sea level. Calculate the induced drag for this wing.

[Answer: 969.44 N]

12. A free vortex flow field is given by v = , for r > 0. If the flow density p = 103 kg/m3 and the

2nr

volume flow rate q = 20n m2/s, express the radial pressure gradient, dp/dr, as a function of radial distance r, and determine the pressure change between ri = 1m and r2 = 2 m.

Answer: —r^, 37.5 kPa

r3

13. A viscous incompressible fluid is in a two-dimensional motion in circles about the origin with tangential velocity:

1 (r2

Щ = – f — r vt

where v is kinematic velocity and t is time. Find the vorticity f.

14.

A circular cylinder of radius a is in an otherwise uniform stream of inviscid fluid but with a positive circulation round the cylinder, as shown in Figure 5.60. Find the lift and drag per unit span of the cylinder. Also, sketch the streamlines around the cylinder if the circulation is subcritical.

[Answer: lift = рУ^Г, drag = 0]

15. A square ring vortex of side 2a. If each side has strength Г, calculate the velocity induced at the center of the ring.

V2

Answer: — Г

References

1. Rathakrishnan, E., Fluid Mechanics – An Introduction, 3rd edn. PHI Learning, New Delhi, 2012.

2. Milne-Thomson, L. M., Theoretical Aerodynamics, 2nd edn. Macmillan & Co., Ltd, London, 1952.

3. Lamb, H., Hydrodynamics, 6th edn. Dover Publications, 1932.

4. Rathakrishnan, E., Applied Gas Dynamics, John Wiley, NJ, 2010.