Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Local Separated Flow Past a Flap (Endplate)
When modelling power-augmented lifting flows by using flow schemes 1 or 3 (see Figs. 8.1 and 8.3), it is necessary to have a solution of the flow problem for the jet escaping from under the flap or the endplate. Earlier, some results of the solution of this problem by Gurevich [138] were used for determining the contraction of the escaping jet and of the pressure drag component due to the rear flap. Here we give a complete solution of this local problem by a method different from [138]; see Fridman [157]. Note that knowledge of characteristics of this type of local flow is quite practical because both available experimental data and theoretical results show the significant influence of effective gaps under endplates and flaps upon the efficiency of cruise and power-augmented modes of motion. In addition, the structure of equation (4.53) and expressions for determining the aerodynamic centers and static stability criteria show that it is possible to control both the lifting capacity and the stability of longitudinal motion by devices that provide variation (chordwise and in time) of the gaps under the endplates.3
The flow problem under consideration and the corresponding auxiliary plane £ are depicted in Fig. 8.6 with designations : X = x/h,Y = y/h\ the stretched length of the device is bf = bi/h for the flap and hep(x) = hep(x)/hi(x) for the endplate. In the latter case, hep and h are the local length of the endplate and the local ground clearance of the wing at the cross section x = const.
|
The complex conjugate velocity in the auxiliary plane isExpression (8.40) determines the width of the effective gap |
and the flow |
|
contraction factor. We evaluate the behavior of the free surface far from the flap (endplate). On part of the boundary in the auxiliary plane, corresponding to the free surface (|AB|), rj = 0. Therefore, |
2fb(0 = -N ^ 4, c2 £Zl) ^ – 6f exP(Wf/^)»
 |
 |
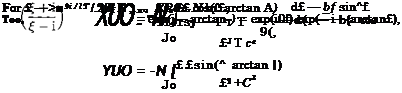where £ Є [0, oo). Taking into account the identity
Therefore,
Y{s ~ -1 + Sf + — exp(Xfs/N). (8.46)
7Г
The latter result shows that for the escaping flow under a flap or an end – plate, Xu —> —oo, the jet boundary resolves into a horizontal line exponentially. From the physical viewpoint, this means that perturbed zero pressure conditions apply immediately outside of the flap or the endplate.
