Parasite Drag

Parasite drag – the drag of the many parts of a helicopter, such as the fuselage, rotor head, landing gear, tail rotor and tail surfaces, which make no direct contribution to main rotor lift – becomes a dominant factor in aircraft performance at the upper end of the forward speed range. Clearly the incentive to reduce parasite drag grows as emphasis is placed on speed achievement or on fuel economy. Equally clearly, since the contributing items all have individual functions of a practical nature, their design tends to be governed by practical considerations rather than by aerodynamic desiderata. Recommendations for streamlining, taken on their own, tend to have a somewhat hollow ring. What the research aerodynamicist can and must do, however, is provide an adequate background of reliable information which allows a designer to calculate and understand the items of parasite drag as they relate to their particular requirement and so review their options.

Such a background has been accumulated through the years and much of what is required can be obtained from review papers, of which an excellent example is that of Keys and Wiesner [10]. These authors have provided, by means of experimental data presented non-dimensionally, values of fuselage shape parameters that serve as targets for good aerodynamic design. These include such items as corner radii of the fuselage nose section, fuselage cross-section shape, afterbody taper and fuselage camber. Guidelines are given for calculating the drag of engine nacelles and protuberances such as aerials, lights and handholds. Particular attention is paid to the trends of landing-gear drag for wheels or skids, exposed or faired. Obviously the best solution for reducing the drag of landing gear is full retraction, which, however, adds significantly to aircraft weight. Keys and Wiesner have put this problem into perspective by means of a specimen calculation, which for a given mission estimates the minimum flight speed above which retraction shows a net benefit. The longer the mission, the lower the break­even speed.

The largest single item in parasite drag is normally the contribution from the rotor head, known also briefly as hub drag. This relates to the driving mechanism between rotor shaft and

blades, illustrated in Figure 6.29, and includes as drag components the hub itself, the shanks linking hub to blades, the hinge and feathering mechanisms and the control rods. Convention­ally all these components are non-streamlined parts creating large regions of separated flow and giving a total drag greater than that of the basic fuselage, despite their much smaller dimensions. The drag of an articulated head may amount to 40% or 50% of total parasite drag, that of a hingeless head to about 30%. The application of aerodynamic fairings is possible to a degree, the more so with hingeless than with articulated heads, but is limited by the relative motions required between parts.

Sheehy [11] conducted a review of drag data on rotor heads from US sources and showed that projected frontal area was the determining factor for unfaired heads. Additionally, allowance had to be made for the effects of local dynamic pressure and head-fuselage interference, both of which factors increased the drag. Fairings needed to be aerodynamically sealed, especially at the head-fuselage junction. The effect of head rotation on drag was negligible for unfaired heads and variable for faired heads. The determination of helicopter hub drag is a very complex process and is often achieved by wind tunnel testing. A typical installation is shown in Figure 6.30.

Picking up the lines of Sheehy’s review, a systematic series of wind tunnel model tests was made at Bristol University [12], in which a simulated rotor head was built up in stages. The drag results are summarized in Figure 6.31.

An expression for rotor head drag D emerges in the form:

with the following definitions.

q0 is the free stream dynamic pressure X/2pV’^. q is the local dynamic pressure at the hub position, measured in absence of the rotor head. In a general case, the local supervelocity and hence q can be calculated from a knowledge of the fuselage shape.

CD is the effective drag coefficient of the bluff shapes making up the head. This may be assumed to be the same as for a circular cylinder at the same mean Reynolds number. For the

Pathfinder fuselage model in University of Southampton 11 ft by 8 ft wind tunnel

Figure 6.30

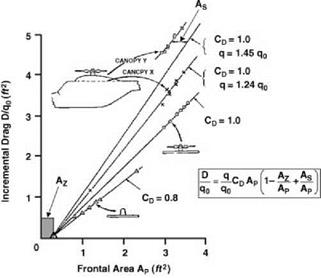results of Figure 6.31 it is seen that a value CD = 1.0 fits the experimental data well, apart from an analytically interesting butunreal case of the hub without shanks, where the higher Reynolds number of the large-diameter unit is reflected in a lower CD value. In default of more precise information it is suggested that the value CD = 1.0 should be used for general estimation purposes. One might expect the larger Reynolds number of a full-scale head to give a lower drag coefficient, but the suggestion rests to a degree on Sheehy’s comment that small-scale model tests tend to undervalue the full-scale drag, probably because of difficulties of accurately modelling the head details.

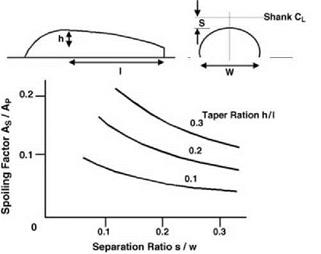
Figure 6.32 Chart for estimating spoiling factor AS

AP is the projected frontal area of the head, as used by Sheehy. AZ represents a relieving factor on the drag, illustrated in Figure 6.31 and resulting from the fact that the head is partly immersed in the fuselage boundary layer. In magnitude AZ turns out to be equal to the projected area contained in a single thickness of the boundary layer as estimated in absence of the head. The last quantity AS represents in equivalent area terms the flow spoiling effect of the head on the canopy. This is a function jointly of the separation distance of the blade shanks above the canopy (the smaller the separation, the greater the spoiling) and the taper ratio of the canopy afterbody (the sharper the taper, the greater the spoiling). The ratio AS/AP may be estimated from the chart given in Figure 6.32 constructed by interpolation from the results for different canopies tested.

In light of the evidence quoted, the situation on rotor head drag may be summed up in the following points:

• The high drag of unfaired rotor heads is explained in terms of exposed frontal area and interference effects and can be calculated approximately for a given case.

• Hingeless systems have significantly lower rotor head drag than articulated systems.

• The scope for aerodynamic fairings is limited by the mechanical nature of the systems but some fairings are practical, more especially with hingeless rotors, and can give useful drag reductions.

• The development of head design concepts having smaller exposed frontal areas carries considerable aerodynamic benefit.