Solution of the General Equation

The problem now is to express the vorticity distribution k as some expression in terms of the camber line shape. Another method of finding kdx is to utilize the method of Equation (6.9), where simple expressions can be found for the velocity distribution around skeleton aerofoils. The present approach is to work up to the general case through particular skeleton shapes that do provide such simple expressions, and then apply the general case to some practical considerations.

6.1.1 Thin Symmetrical Flat Plate Aerofoil

For a flat plate, dy/dx = 0. Therefore, the general equation [Equation (6.9)] simplifies to:

1 fc kdx

Ua = — ———- .

2n J0 —x + X1

It is convenient to express the variable x in terms of в, through:

c

x = — (1 — cos в)

and x1 in terms of в1 as:

c

x1 = ^(1 — cos в1).

The integration limits of Equation (6.10) become:

в varies from 0 to n (that is, 0 < в < n) as x varies from 0 to c (that is, 0 < x < c)

and

dx = – sin в de. 2

Equation (6.10) becomes:

A value of k which satisfies Equation (6.11) is:

(1 + cos в)
sin в

Therefore:

1	Г
Ua = — 2n	.1
Ua	,n
n	0
Ua	(n).
n

2Uasin в(1 + cos в)dв sin в (cos в — cos в[) (1 + cos в) dв cos в — cos в1

A more direct method for getting the vorticity distribution k is found as follows.

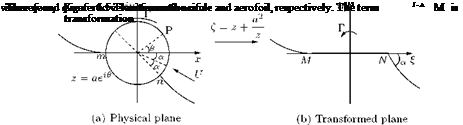
Transformation of the circle z = aelB, through the Joukowski transformation Z = z + , to a lifting

flat plate section at an incident angle a requires by the Joukowski hypothesis that sufficient circulation be

imposed to bring the rear stagnation point down to m on the cylinder, as shown in Figure 6.5(a), where the velocity at a given point P(a, в) is:

qa =

that is:

For small a this simplifies to:

The variable в in Equation (6.13) is the same as that used in the general equation [Equation (6.11)]. This can be easily shown by shifting the axes in Figure 6.5(b) to the leading edge and measuring x rearward. When the chord c = 4a, the distance x becomes:

c

= 2

c

= 2 (1 – cos в) .

Then taking:

k — qa1 qa2 .

where qa1 is the velocity at the point where в = в1 and qa2 is the velocity at the same point on the other side of the aerofoil where в = —в. Therefore:

Thus, in general, the elementary circulation at any point on the flat plate is:

Example 6.1

(a) Find the circulation at the mid-point of a flat plate at 2° to a freestream of speed 30 m/s.

(b) Will this be greater than or less than the circulation at the quarter chord point?

Solution

(a) Given, a = 2°, U = 30 m/s.

At the mid-point of the plate в = n/2.

Circulation around a plate at a small angle of incidence, by Equation (6.14), is:

At в = n/2, the circulation is:

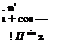
k = 2 x 30 x (2 x 180)

(b) The coordinate along the plate is:

§ = 2b cos в.

At the quarter chord point, § = 3b/4, since chord is 4b and the chord is measured from в = n, that is, from the trailing edge. Thus:

3b/4 = 2b cos в 3

в = cos
= 68°.

Therefore, the circulation at the quarter chord point becomes:

, n /1 + cos 68°

k = 2 x 30 x 2 x ——— ) x ——————

18^ V sin 68°

= 3.105 m2/s.

The circulation at the quarter chord point is greater than that at the middle of the plate.