The Aerodynamic Coefficients for a Flat Plate
The expression for k can be put in the equations for lift and pitching moment, by using the pressure:
(1 cos в)
p = pUk = 2pU2a—————– . (6.15)
sin в
It is to be noted that:
• Full circulation is involved in k.
• The circulation k vanishes at the trailing edge, where x = c and в = n. This must necessarily be so for the velocity at the trailing edge to be finite.
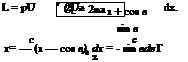 |
||
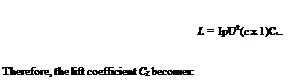 |
![]()
 |
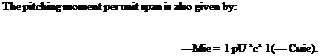 |
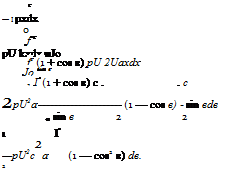
The lift per unit span is given by:
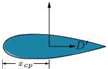
For small values of angle of attack, a, the center of pressure coefficient, kcp, (defined as the ratio of the center of pressure from the leading edge of the chord to the length is chord), is given by:
This shows that the center of pressure, which is a fixed point, coincides with the aerodynamic center. This is true for any symmetrical aerofoil section. The resultant force at the leading edge, at the quarter chord point and the center of pressure of a symmetrical aerofoil are shown in Figure 6.6.
 |
 |
|
By inspection, the quantitative relation between the three cases shown in Figure 6.6 can be expressed as:
Figure 6.6 Resultant force on a symmetrical aerofoil.
Thus, the momentum coefficient about the quarter-chord point is:
This is the theoretical result that “the center of pressure is at the quarter-chord point for a symmetrical aerofoil.”
By definition the point on the aerofoil where the moments are independent of angle of attack is called the aerodynamic center. The point from the leading edge of the aerofoil at which the resultant pressure acts is called the center of pressure. In other words, center of pressure is the point where line of action of the lift L meets the chord. Thus the position of the center of pressure depends on the particular choice of chord.
The center of pressure coefficient is defined as the ratio of the center of pressure from the leading edge of the aerofoil to the length of chord. This is represented by the symbol kcp. One of the desirable properties of an aerofoil is that the travel of center of pressure in the working range of incidence (that is from zero-lift incidence to the stalling incidence) should not be large. As incidence increases the center of pressure moves towards the quarter-chord point.
From the above result, it is seen that the moment about the quarter-chord point is zero for all values of a. Hence, for a symmetrical aerofoil, we have the theoretical result that “the quarter-chord point is both the center of pressure and the aerodynamic center.” In other words, for a symmetrical aerofoil the center of pressure and aerodynamic center overlap. That is, for a symmetrical aerofoil the center of pressure and aerodynamic center coincide.
The relative position of center of pressure cp and aerodynamic center ac plays a vital role in the stability and control of aircraft. Let us have a closer look at the positions of cp and ac, shown in Figure 6.7.
We know that the aerodynamic center is located around the quarter chord point, whereas the center of pressure is a moving point, strongly influenced by the angle of attack. When the center of pressure is aft of aerodynamic center, as shown in Figure 6.7(a), the aircraft will experience a nose-down pitching moment. When the center of pressure is ahead of aerodynamic center, as shown in Figure 6.7(b), the aircraft will experience a nose-up pitching moment. When the center of pressure coincided with the aerodynamic center, as shown in Figure 6.7(c), the aircraft becomes neutrally stable.
From our discussions on center of pressure and aerodynamic center, the following can be inferred:
• “Center of pressure” is the point at which the pressure distribution can be considered to act-analogous to the “center of gravity” as the point at which the force of gravity can be considered to act.
• The concept of the “aerodynamic center” on the other hand, is not very intuitive. Because the lift and location of the center of pressure on an airfoil both vary linearly (more or less) with angle of attack, a, at least within the unstalled range of a. That is we can define a point on the chord of the airfoil at which the pitching moment remains “constant,” regardless of the a. That point is usually near the quarter-chord point and for a symmetrical airfoil the constant pitching moment would be zero. For a cambered airfoil the pitching moment about the aerodynamic center would be nonzero, but constant. The usefulness of the aerodynamic center is in stability and control analysis where the aircraft can be defined in terms of the wing and tail aerodynamic centers and the required lift and moments calculated without worrying about the shift in center of pressure with a.
The horizontal position of the center of gravity has a great effect on the static stability of the wing, and hence, the static stability of the entire aircraft. If the center of gravity is sufficiently forward of the aerodynamic center, then the aircraft is statically stable. If the center of gravity of the aircraft is moved toward the tail sufficiently, there is a point – the neutral point – where the moment curve becomes horizontal; this aircraft is neutrally stable. If the center of gravity is moved farther back, the moment curve has positive slope, and the aircraft is longitudinally unstable. Likewise, if the center of gravity is moved forward toward the nose too far, the pilot will not be able to generate enough force on the tail to raise the angle of attack to achieve the maximum lift coefficient.
The horizontal tail is the main controllable moment contributor to the complete aircraft moment curve. A larger horizontal tail will give a more statically stable aircraft than a smaller tail (assuming, as is the normal case, that the horizontal tail lies behind the center of gravity of the aircraft). Of course, its distance from the center of gravity is important. The farther away from the center of gravity it is, the more it enhances the static stability of the aircraft. The tail efficiency factor depends on the tail location with respect to the aircraft wake and slipstream of the engine, and power effects. By design it is made as close to 100% efficiency as possible for most static stability.
Finally, with respect to the tail, the downwash from the wing is of considerable importance. Air is deflected downward when it leaves a wing, and this deflection of air results in the wing reaction force or lift. This deflected air flows rearward and hits the horizontal-tail plane. If the aircraft is disturbed, it will change its angle of attack and hence the downwash angle. The degree to which it changes directly affects the tail’s effectiveness. Hence, it will reduce the stability of the airplane. For this reason, the horizontal tail is often located in a location such that it is exposed to as little downwash as possible, such as high on the tail assembly.











