Comparison of Several Model Order Criteria
The crucial aspect of time-series modeling is that of selection of model structure (AR, MA, ARMA, or LS) and the number of coefficients for fitting this model to the time-series data. There are several model order selection criteria available in the literature [1,10]. Selection of a reliable and efficient test criterion could be difficult, since most criteria are sensitive to process-statistical properties, which are often unknown. In the absence of a priori knowledge, any system that is generating time-series output data/signals could be represented by the more popular AR or LS model structures. These structures represent a general nth order discrete linear time-invariant system affected by random noise. The problem of model order determination is to assign a model dimension to adequately represent the unknown system, and the model selection procedure involves selecting a model structure and its complexity. Often a model structure can be ascertained based on the knowledge of the physics of the system. For certain processes, if physics is not well understood, then a black-box approach can be used, leading to a trial and error iterative procedure. In many situations, some knowledge about the system or the process would be available. Several model selection criteria arising out of different, but sometimes related, principles of goodness of fit and statistical measures are possible. The criteria based on fit error of estimation, number of model parameters/coefficients, and whiteness of residuals are given in Table 9.1.
|
TABLE 9.1 Comparison of Some Model Order Selection Criteria
|
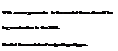 |
TABLE 9.1 (continued)

![]()
![]()
![]()
![]()
 If the two models are equally likely (L1 ~ L2), then the one with less number of parameters is chosen again according to the principle of parsimony. If the number of parameters increases, the AIC also increases, and hence the model is less preferable.
If the two models are equally likely (L1 ~ L2), then the one with less number of parameters is chosen again according to the principle of parsimony. If the number of parameters increases, the AIC also increases, and hence the model is less preferable.
The test based on whiteness of residuals is widely used to check whether the residuals of fit are a white noise sequence. Autocorrelation based whiteness of residuals (ACWRT) test is performed as shown in Table 9.1. Here, it is assumed that r(k) is a zero mean sequence. Autocorrelations must lie in the band ±1.96 Д/N at least for 95% of the time for the null hypothesis and usually the normalized ratio is used: Rrr(r)/Rrr(0). Autocorrelations tend to be impulse function if the residuals are uncorrelated, and hence at other times their values must be too small, within the above-prescribed bounds. For input/output (I/O) type models (ARMA, transfer function [LS]), the process of cancellation of zeros with poles provides a model with less complexity. The numerator and denominator polynomials are factored and cancellation, if any, then becomes obvious, but a subjective judgment is involved, since the cancellation might not be perfect. Often eigenvalues are used for model reduction and selection. Eigenvalues cannot be meaningfully determined for a covariance matrix if I/O units differ. Dimensional inconsistencies can be removed
by appropriate normalization of the covariance matrices used in the computation of model order criteria.
Detailed modeling using time-series and transfer function analysis is covered in Ref. [10], wherein three applications of model order determination are considered. The data sets were derived from (1) a simulated second-order system, (2) experiments with a human operator in a fixed-base simulator, and (3) forces on a scaled-down model of an aircraft in a wind tunnel exposed to mildly turbulent flows. For the simulated system, AR model identification was carried out using the LS method and it was found that several model order criteria, studied in the foregoing, provided sharp and consistent decisions. Next, the time-series data for the human operator’s responses were derived from a compensatory manual control tracking experiment on a fix-base research flight simulator. Before recording the data the operator was allowed to reach his steady performance in the tracking task. The LS/AR models were fitted to the data and several model order determination criteria were used and studied. Five hundred data points sampled at 50 ms were used for SID. A fifth-/sixth-order AR model for human activity in the tracking task was found suitable, whereas the LS model of second order was found to be also suitable for the same data sets as can be seen from Table 9.2.
From the discrete Bode diagrams obtained for the LS models, it was found that adequate amplitude ratio (plot vs. frequency) was obtained for the second-order TF. Thus, the AR pilot model differs from the LS pilot model in model order because the LS model has distinct I/O structure and hence the data is well captured by the numerator also. This is not so for the AR model and hence a longer (large order) model is required. Estimation of pitch damping derivatives was attempted using random flow fluctuations inherent in the tunnel flow, wherein an aircraft’s scaled physical model was mounted on a single DOF flexure with a dominant second-order response. The excitation to the model was inaccessible and not measurable, being the random flow fluctuation of the tunnel itself. AR models were fitted using 1000 sample data. Since response was known to be of second order, the natural frequency was determined by evaluating the spectra using a frequency transformation of discrete AR models. The estimated natural frequency stabilized for AR(n), n > 10.
Based on the experience gained, using several model order criteria, the following working rule is considered adequate for selection of the model order to fit varieties of experimental data. For order determination: (1) evaluate entropy criterion (AR only), (2) evaluate FPE, (3) perform F-test, and (4) check for pole-zero cancellations (for I/O model). For model validation: (1) see time-history prediction, (2) test residuals for whiteness, and (3) do the cross validation.
|
TABLE 9.2 Human Operator’s LS Model from the Tracking Experiments
|











