Simplified Aerodynamics Models

Following the helicopter theory, a simplified analysis for flapping flight can be estab­lished based on the actuator disk model. An actuator is an idealized surface that continuously pushes air and imparts momentum to downstream by maintaining a pressure difference across itself (i. e., the lift is equal to the change in fluid momen­tum). Assuming that insect wings beat at high enough frequencies so that their stroke planes approximate an actuator disk, the wake downstream of a flapping wing can be modeled as a jet with a uniform velocity distribution [65] [338]. Although the momentum theory accounts for both axial and rotational changes in the velocities at the disk, it neglects the time dependency in wing shape, kinematics, and associated unsteady lift-producing mechanisms.

By using the Bernoulli equation for steady flow to calculate induced velocity at the actuator disk and the jet velocity in the far wake downstream (i. e., the downwash), Weis-Fogh [339] derived the induced downwash velocity wi for a hovering insect at the stroke plane as

w (3-24)

where Wis the insect weight, p the air density, and R the wing length. From the exper­imental measurements of the beetle Melolontha vulgaris Weis-Fogh [339] assumed that the downwash velocity in the far wake is twice that at the disk (i. e., w = 2wi), even though he pointed out that wi varies through a half-stroke and that stroke plane amplitude Ф is rarely 180°.

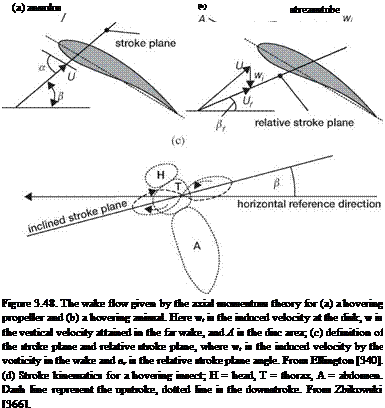
Instead of using a circular disk, Ellington [340] proposed a partial actuator disk of the area A = ФR2 cos (в) that flapping wings cover on the stroke plane, as depicted in Figure 3.48, and modified the expression for the induced power Pind, such that

p-=GR^)=w Ш) • (3-25)

where в is the stroke plane angle and WI A is the disk loading that controls the minimum power requirement. He also noted that, because of the time-varying nature of flapping, a pulsed actuator disk seems more representative of hovering flight. He showed that the circulation of the vortex rings in the far wake downstream is related to the jet velocity:

where fs is the shedding frequency.

Rayner [79] [ 341] proposed a method representing the wake of a hovering insect by a chain of small-cored coaxial vortex rings (one produced for each half-stroke). Although the approach could determine the lift and drag coefficients, it did not account for the effects of stroke amplitude and stroke plane angle. Sunada and Ellington [293] developed a method that models the shed vortex sheets in the wake as a grid of small vortex rings, with the shape of the grid modeled by wing kinematics so that all forward speeds can be handled.

Overall, the relatively simple approaches presented in this section are of limited usefulness because they only include stroke-plane angle and disk loading. The models do not allow, for example, estimation of lift forces for a given wing kinematics or wing geometry.

One way to estimate the force generation is to measure the vorticity ы in the flow field around the flapping wing. Then, for steady inviscid irrotational (potential) flow, the lift per unit span on such a wing can be approximated as

L = PU^r’

where UTO is the free-stream velocity and Г is the circulation over the flow field S, defined as

Because obtaining a direct pressure measurement over a moving wing is difficult, applying Eq. (3-27) has been a popular way to estimate the lift generation. However, the so-called wake momentum paradox arose when the lift generation of slow – flying pigeons [342] and jackaws [343] appeared to be only 50 percent of the force that is required to sustain their weight. Later using high-resolution wake vorticity measurements and by accounting for all vortical structures Spedding et al. [344] showed that the resulting wake structures provide sufficient momentum for weight support. Another caveat is that Eq. (3-27) is only valid for steady-state flow field around a stationary wing. When the wing and its wake change in time, the unsteady

term in the momentum conservation needs to be correctly accounted for, as shown by Noca et al. [345], which we discuss in detail in Section 3.6.4.

In the quasi-steady approach, the lift and drag force coefficients are computed based on the steady-state theory while varying the geometry and speed in time. To account for the variations in velocity and geometry from wing base to tip, the blade-element approach has been followed to discretize the wing into chordwise, thin wing strips; the total force is computed by summation of the forces associated with individual strips along the spanwise direction [65] [ 294]. Integrating lift over the entire stroke cycle gives the total lift production of the flapping wings. For example, considering such wing kinematics and wing geometry, Osborne [294] proposed a quasi-steady approach to model insect flight: the forces acting on the insect wing at any point in time are assumed to be the steady-state values that would be achieved by the wing at the same velocity and AoA. Later, in 1956, Weis-Fogh and Jensen [346] laid out the basis of momentum and blade-element theories as applicable to insect flight and carried out quantitative analyses on wing motion and energetics available at the time. Their results indicated that, in most cases, when forward flight is considered, the quasi-steady approach appears to hold for the reason that, as flight velocity increases, unsteady effects diminish. In the mid-1980s, Ellington published a series of papers on insect flight [65] [ 70] [ 340] [ 347]-[349]. He presented theoretical models for insect flight by using actuator disks [340]; vortex wake [340]; quasi-steady methods [65]; rotation-based mechanisms of clap, peel, and fling [340]; and insights into unsteady aerodynamics [340] [349].

From the blade-element method, Ellington combined expressions for lift due to translational and rotational phases. Using the thin airfoil theory and the Kutta – Joukowski theorem (Eq. (3-27)), he derived the bound circulation as

Г = n cU sin ae, (3-29)

where c is the chord length, U is the incident velocity, and ae is the effective AoA corrected for profile shape. Following Fung’s method [350], he also derived an expression for circulation due to rotational motion by computing incident velocity at the 3/4 chord point while satisfying the Kutta-Joukowski condition, giving

Г = жаc2 3 – *0 , (3-30)

where a is the rotational (pitching) angular velocity and x0 is the distance from the leading edge to the point about which rotation is being made (pitch axis), normalized with respect to the chord c. Combining Eqs. (3-29) and (3-30), Ellington obtained the quasi-steady lift coefficient:

Equation (3-31) is equivalent to Theodorsen’s formula for lift: Eq. (3-21) in the quasi-steady limit (i. e., C(k) = 1) without the added mass components. Although Osborne [294] suggested that the added mass may play an important role in flapping wing flight, Ellington [348] argued that the additional time-averaged lift due to the added mass (virtual mass) vanishes for periodic motions. The additional drag due to added mass is also zero because there is no net wing acceleration parallel to the wing
stroke during a motion period. Recently, Kang et al. [351] normalized the integral form of the Navier-Stokes equation and proposed that the added mass effects are important for the high reduced frequency and high Reynolds number flows. In particular, the added mass force should not be neglected when investigating the performance of a flexible flapping wing in a high-density medium, such as in water. Furthermore, to determine lift and power requirements for hovering flight, Ellington [349] sought estimates for the mean lift coefficient through the flapping cycle and derived a non-dimensional parameter-based expression:

(3-32)

where {L) is the mean lift through a half-stroke, p is the air density, f is the wing-beat frequency, Ф is the stroke angle, {(d<f>/dt)2) is the mean-squared flapping angular velocity, S is the wing area, в is the stroke plane angle, вг is the relative stroke plane angle (see Fig. 3.48c), and r2 is the second moment of the wing area.

Numerous versions of the quasi-steady approach can be found in the literature; in general, the model predictions are not consistent with the physical measurements, especially when the hovering flight of insects is considered. For example, lift coef­ficients obtained under those conditions yield (i) 0.93-1.15 for dragonfly Aeschna juncea [229] [352], (ii) 0.7-0.78 for fruit fly Drosophila [353] [354], and (iii) 0.69 for bumblebee Bombus terrestris [212]. However, lift coefficients estimated by direct force measurements in flying insects are significantly larger than those predicted by the quasi-steady methods, ranging from 1.2 to 4 for various insects including the hawkmoth Manduca sexta, bumblebee Bombus terrestris, parasitic wasp Encar – sia formosa, dragonfly Aeschna juncea, and fruit fly Drosophila melanogaster [339] [349] [355] [356].

Because quasi-steady methods are unable to predict flapping wing aerodynamics accurately, empirical corrections have been introduced. Walker and Westneat [357] presented a semi-empirical model for insect-like flapping flight, which includes, for example, Wagner’s function [350], which is devised to account for the lift enhance­ment caused by an impulsively starting airfoil. They used a blade-element method to discretize the flapping wing and then computed forces on the wing elements, in which the forces comprise a circulation-based component and a non-circulatory apparent mass contribution. Sane and Dickinson [216] refined a quasi-steady model to describe the forces measured in their earlier experiments on the Robofly, a mechanical, scaled – up model of the fruit fly Drosophila melanogaster [228]. They decomposed the total force F into four components, namely,

F — Ft + Fr + Fa + Fw,

where the subscripts t and r are for translational and rotational quasi-steady com­ponents, respectively; a is for added mass; and w is for wake capture. In the blade – element approach, a Robofly wing is divided along the spanwise direction into chord – wise strips, and the forces on each strip are computed individually and integrated along the span. The translational quasi-steady force Ft is computed from empirically fitted equations from a 180° sweep with fixed AoAs as

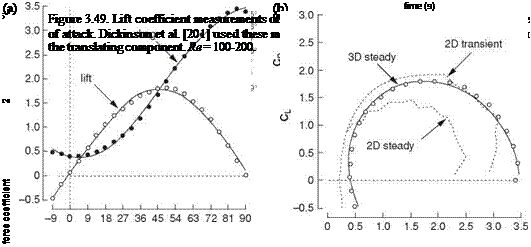
CL — 0.225 + 1.58 sin(2.13a – 7.2),

angle of attack (degrees) CD

CD = 1.92 – 1.55 cos(2.04a – 9.82), (3-34)

see also Figure 3.49. To determine the rotational quasi-steady force Fr, Sane and Dickinson [216] set the forces due to added mass and wake capture to zero (i. e., Fa = Fw = 0) by removing any accelerations and avoiding wake reentry, respectively. They measured the force F acting on a wing undergoing a constant translation and rotation for one forward stroke only and obtained the rotational force Fr by subtracting the empirically predicted translational force Ft from the measured total force F. For the quasi-steady treatment of the rotational force they used Eq. (3-34) and replaced the free-stream velocity with the instantaneous translation velocity, Ut, as Fr = CrotpUtTr, with Crot being a coefficient that depends on the angular velocity. Furthermore, they computed the added mass Fa by applying the added mass term from the linearized aerodynamic theories (e. g., Eq. (3-21)), for each blade element and integrating along the span. Knowing these three components, they evaluated the wake-capture force Fw by subtracting the components Ft, Fr, and Fa from the total measured force F. The wake-capture force arises from the interaction with the wakes and vortices shed in the previous strokes. At the beginning of the stroke, the enhanced momentum increases lift as described in Section 3.3.1. In contrast,
during the mid-stroke the effects of the wing-wake interaction are negative due to the downwash, which resides upstream of the wing generated by the wakes shed in the previous strokes [358] [359]. As the wing starts to interact with this downward wake, the effective angle of attack reduces.

Kang and Shyy [359] combined the geometric angle of attack and this down – wash to calculate an effective angle of attack, which is fed in the lift estimation of the translational component, Eq. (3-34). The translational lift corrected for the down – wash indeed predicted a loss of lift during this part of the stroke, thereby giving a better approximation of the lift calculated by solving the Navier-Stokes equations. Further discussion can be found in Section 4.5.1. Wing-wake interaction depends on the history and non-linear aerodynamic effects, and an a priori estimation of this force due to wing-wake interaction has still not been found.

A model for unsteady lift generation for insect-like flapping wings was proposed by Pendersen and Zbikowski [360]. The model is modular, giving a better insight into various effects on aerodynamic force generation, and it includes added mass effects, the quasi-steady assumption, an LEV effect, and the wake effect. The model’s predicted lift and drag forces were compared with the measurements of Dickinson et al. [201], and despite its simplifications, the model captures reasonably well the lift evolution, but over-predicts the force peak values.

Although such semi-empirical methods can be tuned to provide good agree­ment with experimental measurements, their predictable capabilities are question­able because they cannot adequately account for the relevant unsteady, vortical fluid physics. In particular, the unsteady effects are important not only during the translational phases of the stroke (upstroke and downstroke) but also during the rotational phase near the end of each stroke when the wings are quickly rotated around their spanwise axes [247] [275] [229] [361]. Nevertheless, the quasi-steady model does provide some insight into flapping flight in insects and birds and offers quick estimates of unsteady aerodynamic coefficients.

Recently, Ansari et al. [362] [363] modified and extended the circulation approach for modeling insect-like flapping wings in the hover. It is based on the origi­nal approach of von Karman and Sears [332] together with the non-linear extensions proposed by McCune et al. [364] and Tavares and McCune [365], but with further significant extensions as well. Ansari et al. [362] [363] showed not only the valid­ity of their unsteady aerodynamic model by comparing it with the experiments of Dickinson et al. [201] but also the limitation of the model (i. e., an inviscid, potential, and essentially 2D model).