Lift, Pitching Moment and Center of Pressure Coefficients for a Thin Aerofoil

From Equation (6.30), the circulation distribution is:

Therefore, the lift becomes:

c

L = pU

П

pU—k sin в de P 2

since:

П

sin в sin пв de = 0 when n = 1.

0

The lift is also given by:

1 2

L = – pU2cCL.

Therefore, the lift coefficient becomes:

The pitching moment is given by:

c

—Mle = pU kxdx

0

1 2 •

= —CMuT. pU c

( 2pU-(c/2)-

Ml‘ ^ 1 pU 2c2

An sin пЄ cos в sin в dв

П П П

= — A0 + — Al — — A2, 2 0 + 2 1 4 2’

since:
sin ив sin шв dO = 0	when и — ш.

Therefore:

A2 Ao + Ai – A
	(6.36)

that is:

The center of pressure coefficient is:

(6.37)

From Equation (6.37) it is seen that for this case also the center of pressure moves as the lift or incidence is changed. We know that the kcp is also given by [Equation (6.19)]:

Comparing Equations (6.36) and (6.37), we get:

This shows that, theoretically, the pitching moment about the quarter chord point for a thin aerofoil is a constant, depending on the camber parameters only, and the quarter chord point is therefore the aerodynamic center.

Example 6.4

The camberline of a thin aerofoil is given by:

y — kx(x – 1)(x – 2),

where x and y are in terms of unit chord and the origin is at the leading edge. If the maximum camber is 2.2% of chord, determine the lift coefficient and the pitching moment coefficient when the angle of attack is 4°.

Solution

Given, camber is 0.022 and a = 4°.

At the maximum camber location, let x = xm. At the maximum camber:

^ = 0,

dx

that is:

k (3xi – 6xm + 2) = 0 3xi – 6x„ + 2 = 0

6 ± V36 – 24
6

1 ± 0.577.

Out of the above two values of 1.577 and 0.423, the second one is the only feasible solution for xm. Therefore, the maximum camber is at xm = 0.423. Substituting this we have:

k[xm(xm – 1)(xm – 2)] = 0.022

k[0.423 x (-0.577) x (-1.577)] = 0.022

But:

(1 – cos в) = 2

Substituting this, we get:

— = – ІЗ cos2 в + 6 cos в – 1І. dx 4 L J

By Equation (6.32):

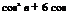
1

A0 = a——

n

в – 1] de

= a –

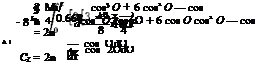33

— k—- k

2 8

Note: The moment is given with a negative sign because this is a nose-down moment.

Example 6.5

A sail plane of wing span 18 m, aspect ratio 16 and taper ratio 0.3 is in level fight at an altitude where the relative density is 0.7. The true air speed measured by an error free air speed indicator is 116 km/h. The lift and drag acting on the wing are 3920 N and 160 N, respectively. The pitching moment coefficient about the quarter chord point is —0.03. Calculate the mean chord and the lift and drag coefficients, based on the wing area and mean chord. Also, calculate the pitching moment about the leading edge of the wing.

Solution

Given 2b = 18 m, = 16, Xt/Xr = 0.3, a = 0.7, L = 3920 N, D = 160 N, Vr = 116 km/h, CMc/4 = -0.03.

The relative density is:

P m a = — = 0.7,

P0

where p0 is the sea level density, equal to 1.225 kg/m3. Therefore:

p = 0.7 P0 = 0.7 x 1.225 = 0.858 kg/m3.

Equivalent air speed is:

V07

= 138.65 km/h _ 138.65 = 3.6

= 38.51 m/s.

The mean chord is:

span

2b

M
18

16

The wing area is:

S = 2b x c = 20.25 m2.

The lift coefficient is:

L

2 pV 2S

2 x 3920

0.858 x 38.512 x 20.25 0.304 .

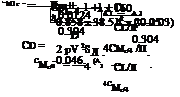By Equation (6.36):

The pitching moment about the leading edge is:

1 2

2 pV2 ScCMu

1 x 0.858 x 38.512 x 20.25 x 1.125 x (—0.046) —666.71 Nm.

The negative sign to the moment implies that it is a nose-down moment.