ML Estimation for Dynamic System

Let a linear dynamical system be described as

X(t) = Ax(t) + Bu(t)	(9.25)
y(t) = Hx(t)	(9.26)
z(k) = y(k) + v(k)	(9.27)

In many applications, the actual systems are of continuous time, but the measure­ments would be at discrete samples, with

E{v(k)} = 0; E{v(k)vT (l)} = R8kl (9.28)

We have the likelihood function as

The parameter vector b is obtained by maximizing the likelihood function with respect to b by minimizing the negative log likelihood function given as

L = – log p(zb, R)

1N

= 2 E [z(k) – y(k)]TR-1 [z(k) – y(k)] + N/2 log R + const (9.30)

2 k=1

The R can be estimated as

When the estimated value R is substituted in the likelihood function, the minimiza­tion of the cost function with respect to b results in

dL/db = – X (dy(b)/db)TR-1(z – y(b)) = 0 (9.32)

k

This set is a system of nonlinear equations and an iterative solution can be obtained by the quasi-linearization method, known as modified Newton-Raphson or Gauss-Newton method. We expand

y(b) = y(b + Db)

as

A version of the quasi-linearization is used for obtaining a workable solution for the OEM.

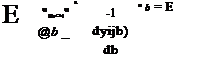Substituting this approximation in Equation 9.34 we get

Ь new — Ь old + Dp

The CRB is a primary criterion for evaluating the accuracy of the estimated param­eters. MLE gives the measure of this parameter accuracy without any extra compu­tation. The information matrix is computed as

The diagonal elements of the inverse of the information matrix give the individual covariance, and the square roots of these elements are measures of the standard deviations called the CRBs. The OEM/MLE can also be applied to any nonlinear system. Computational and accuracy aspects are further discussed in Ref. [і].