The General Thin Aerofoil Section

In Section 6.4, we saw that the general camber line can be replaced by a chordwise distribution of circulation. That is:

к — ka + kb,

where ka is the same as the distribution over the flat plate but must contain a constant (A0) to absorb any difference between the equivalent flat plate and the actual chord line. Therefore:

/1 + cos в

ka — 2UAJ ——- . (6.28)

Y sin в J

Note that this ka distribution satisfies the Kutta-Joukowski distribution, since ka — 0 when в — n, that is, at x — c.

The corresponding kb is represented by a Fourier series. Providing 0 < в < n, the end conditions are satisfied, and any variation in shape is accommodated if it is a sine series. Thus:

kb — 2U (Aj sin в + A2 sin 2в + A3 sin 3в + •• ••)

TO

— 2U ‘y ^ An sin пв. (6.29)

Thus, k — ka + kb becomes:

Note that, for circular arc aerofoil, we have kb — 2UA sin в.

The coefficients A0, A1, A2, • • An can be obtained by substituting for k in the general equation

(6.30), suitably converted with regard to units, that is:

1 fc kdx
dy —— a dx
U
2n	0 X – X1

Substituting:

c

x = — (1 — cos в),

we get:

Using Equation (6.30), we get:

2U Ґ I A0(1 + cos в) I sin ede

— < ^ ——- – + > An sin пв V———————– .

2n J0 I sin в Г cos в — cos в1

At the point x1 (or в1) on the aerofoil:

dy A0 Гn (1 + cos в) d9 1 Гn An sin пв sin в dв

dx n J0 cos в — cos в; n J0 cos в — cos в;

Expressing У] An sin пв sin в as:

‘У ‘ An — [cos (n — 1) в — cos (n + 1) в] ,

we have:

where Gn signifies the integral:

cos nвdв
cos в — cos в1

which has the solution:

n sin nв1
sin в1

Therefore:

dy A0 sin (n — 1) в; — sin (n + 1) в;

—— a =——— n — > An—————————————

dx n -< 2 sin в;

2 (■

cos в) on the aerofoil, we get:

For the general point x

that is:

On integrating from в = 0 to n, the third term on the right-hand-side of Equation (6.31) vanishes. Therefore, we have:

This simplifies to:

Multiplying Equation (6.32) by cos тв, where m is an integer, and integrating with respect to в, we get:

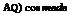dy Ґ,

— cos тв de = (a

dx

The integral: ‘y ^ An cos ив cos тв dв = 0.

for all values of n except at n = m. Therefore, the first term on the right-hand-side of Equation (6.33) vanishes, and also the second term, except for n = m becomes:

An cos пЄ
n = —A„
Thus:
(6.34)
An	— cos пЄ dв dx