Extended Kalman Filtering Algorithm

Many real-life dynamic systems are nonlinear and the estimation of states of such systems is often required. The nonlinear system can be expressed as

x(t) = f [x(t), u(t), Q]	(9.46)
y(t) = h[x(t), u(t), Q]	(9.47)
z(k) = y(k) + v(k)	(9.48)

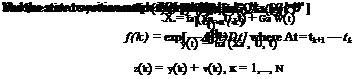variables at time t = 0, bu represents the bias parameters in control inputs, by represents the biases in model responses y, and b represents the parameters in the mathematical model of the system. One needs to linearize the nonlinear functions f and h and apply the KF with proper modifications to these linearized models. The linearizations will be around previous/current best state estimates that are more likely to represent the truth. Simultaneous estimation of states and parameters is achieved by augmenting the state vector with unknown parameters, as additional states, and then using the filtering algorithm with the augmented system nonlinear model. The new augmented state vector is given as

We notice the time-varying nature of A, H, and f because they are evaluated at current state estimate, which varies with time k.

Time Propagation

The states are propagated from the present state to the next time instant. The predicted state is given by

tk+1

The covariance matrix for state error propagates from instant k to k + 1 as

P(k + 1) = f(k)P(k)fT (k) + Ga (k)QGT (k) (9.59)

Measurement Update

The EKF updates the predicted estimates by incorporating the new measurements as follows:

xa(k + 1) = ~a(k + 1) + K(k + 1){Zm(k + 1) – ha[~a(k + 1), u(k + 1), t]} (9.60)

The covariance matrix is updated using the Kalman gain and the linearized meas­urement matrix. The Kalman gain is given by

K(k + 1) = P(k + 1)HT (k + 1)[H(k + 1)P(k + 1)HT (k + 1) + R]-1 (9.61)

The posteriori covariance matrix is given as

P(k + 1) = [/ – K(k + 1)H(k + 1)]P(k + 1) (9.62)

A sophisticated filter error method (FEM) accounts for process and measurement noise using a KF in the structure of the maximum likelihood/OEM (MLOEM). The details of this method are given in Ref. [1].