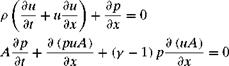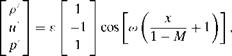Coefficients of Several Large Buffer Stencils

When high-quality, high-order computations are to be performed, one expects that large derivative stencils are to be used in the mesh-size-change buffer region. Opti­mized coefficients of several large buffer stencils are listed below. n is the range of optimization.

9-Point Stencils

1357 derivative stencil. n = 0.885, a0 = 0.0

al = —a-1 = 0.6090238560979105951878503463135849 a3 = — a—3 = —0.04690263734690552411752317530947456 a5 = —a—5 = 7.45976157440795270904970345070725E-3 a7 = — a—7 = —8.021074184619694829327625198139366E-4

1246 derivative stencil. n = 1.075, a0 = 0.0

al = —a—1 = 0.7512246907952941262715227576491948 a2 = —a—2 = —0.1390991789681719362022172210597338 a4 = —a—4 = 7.6185409515963687179825703762642764E-3 a6 = —a—6 = —5.834161108892881231697661724640704E-4

1235 derivative stencil. n = 1.215, a0 = 0.0

al = —a—1 = 0.8080701723801081268126989813400916 a2 = —a—2 = —0.2043432375248032483484509202108968

11-

Point Stencils

13579 derivative stencil. n = 0.96, a0 = 0.0

a3 = – a-1 = 0.6169610748807038603650623876266686 a3 = – a-3 = -0.053037977159713435091000295888159493 a5 = – a-5 = 0.011057680967517392356513295707997069 a7 = – a-7 = -2.2180071199244495954136156095099006E-3 a9 = – a-9 = 2.6561128892451447702970341826597076E-4 12468 derivative stencil. n = 1.15, a0 = 0.0

a3 = – a-1 = 0.7631614437828716630397535144418575 a2 = – a-2 = -0.14840307207850050785201259674573818 a4 = —a-4 = 0.010272925705412492924195271253581683 a6 = — a—6 = —1.4476431210717408970741183395007183E-3 a8 = —a—8 = 1.54857034863728293741913009037069E-4

12357 derivative stencil. n = 1.3, a0 = 0.0

ax = —a—1 = 0.8252543028344873666308890959218707 a2 = — a—2 = —0.2230034607664662190128310868797273

a3 = – a-3 = 0.0434847322758841815894783782752433 a5 = – a-5 = -2.167191168162797315544034817529481E-3 a7 = – a-7 = 1.6205395880093045772258815707159745E-4

12346 derivative stencil. n = 1-4, a0 = 0.0

a3 = – a-1 = 0.8559670270533940785913013975770142 a2 = – a-2 = -0.26355038029346495866745731339388584 a3 = – a-3 = 0.07259552278997621476486631628514457 a4 = —a—4 = -0.012148236925938859899155655963543882 a6 = —a—6 = 3.2335214456043900760615070158323756E-4

13-Point Stencils

1357911 derivative stencil. n = 1.04, a0 = 0.0

a3 = —a—1 = 0.6222744810884503208006161752402352 a3 = —a—3 = —0.05745752283507652911500016054804188 a5 = —a—5 = 0.014048807353574197207816006070727958 a7 = —a—7 = —3.8223706624986957120774761605838786E-3 a9 = —a—9 = 8.773256282094535158374388508297744E-4 an = —a—u = —1.1684412431690283206275822573907119E-4

1246810 derivative stencil. n = 1.225, a0 = 0.0

a3 = —a—1 = 0.7704159669204072987577907570660112 a2 = —a—2 = —0.15423090409941798512572684114924175 a4 = —a—4 = 0.012111428866866974752283356866705977 a6 = — a—6 = —2.237909249412284471498739008161985E-3 a8 = —a—8 = 4.5510386970466766460616813555659377E-4 a10 = — a—10 = —6.132496502028620033274132698325002E-5

123579 derivative stencil. n = 1.375, a0 = 0.0

a3 = —a—1 = 0.8346007521198306780385577274355369 a2 = — a—2 = —0.23351453982173775751336583621371804 a3 = —a—3 = 0.048416204296670338536750729561625173 a5 = —a—5 = —3.0732634681711003723284703258379413E-3 a7 = —a—7 = 4.2764556235837229592649414282684104E-4 a9 = —a—9 = —4.972077355769809243570567373051316E-5

123468 derivative stencil. n = 1.5, a0 = 0.0

a3 = —a—1 = 0.8695040147146564312615709824565512 a2 = —a—2 = —0.28111202563583404799569450627628445

a3 = – a-3 = 0.0845286783216550621158838448960038 a4 = – a-4 = -0.01627930669247656566519371821994323 a6 = -a-6 = 7.921732807092020750043354094040387E-4 a8 = —a—8 = -6.272641528780892588558052108063413E-5

123457 derivative stencil. n = 1.59, a0 = 0.0

ax = —a—1 = 0.8891744805205031441686220773749192 a2 = – a-2 = -0.3096468670894452798278980518929917 a3 = – a-3 = 0.10899054209331996393360155629344859 a4 = —a—4 = -0.030279357225089779657034797121953563 a5 = —a—5 = 5.0487756298281625592780951771430825E-3 a7 = — a—7 = —1.3983169576488149741170426674042277E-4

15-Point Stencils

135791113 derivative stencil. n = 1.11, a0 = 0.0

a3 = —a—1 = 0.6258779354573266902120076920113189 a3 = —a—3 = —0.060595621262294137510257150629882345 a5 = —a—5 = 0.016419419315514504253832969339583166 a7 = —a—7 = —5.332041836769511268442174297083009E-3 a9 = —a—9 = 1.6673308740708772699299319145046008E-3 au = —a—11 = —4.2649198385963323058082868711331986E-4 a13 = — a—13 = 6.31968127067576950549124298229811E-5

124681012 derivative stencil. n = 1.295, a0 = 0.0

a3 = —a—1 = 0.7751653818251308369767154456316511 a2 = —a—2 = —0.15810842159142594570323780970792248 a4 = —a—4 = 0.01344368848930721405861880589370375 a6 = — a—6 = —2.882509303736270724294138583564854E-3 a8 = —a—8 = 7.737358357276028905705620340672378E-4 a10 = — a—10 = —2.0178401810068388499797391894808376E-4 a12 = —a—12 = 3.3309726507986522205418718975874384E-5

12357911 derivative stencil. n = 1.45, a0 = 0.0

a3 = —a—1 = 0.8405083211561195585119035254044648 a2 = —a—2 = —0.24028234117501536764416518113371986 a3 = —a—3 = 0.051710722871922495965649571941564053 a5 = — a—5 = —3.7380739291593315864384143663748303E-3 a7 = —a—7 = 6.732308091610869543962441130822362E-4 a9 = -a-9 = -1.521289737983841685480415909565809E-4 au = – a-11 = 2.464612036347233162080530883553833E-5

12346810 derivative stencil. n = 1-58, a0 = 0.0

a1 = – a-1 = 0.8769697517162914222723512564100425 a2 = —a-2 = -0.2910485506050849365005963442595554 a3 = —a—3 = 0.09160729636798243850623886924431454 a4 = — a—4 = —0.018889586310816595242600622281686327 a6 = —a—6 = 1.1725375731033384971390388407682345E-3 a8 = — a—8 = —1.7648972164255100846899103703416032E-4 a10 = — a—10 = 2.404979677178932654450087545336078E-5

1234579 derivative stencil. n = 1.69, a0 = 0.0

al = —a—1 = 0.8996669663763338312112615547268505 a2 = —a—2 = —0.3248239503161405595421655578148774 a3 = —a—3 = 0.12185450769709449174616083733794719 a4 = — a—4 = —0.03732240294041507819400704949257943 a5 = —a—5 = 7.198430554922608039998318584879614E-3 a7 = —a—7 = —3.6954649492803779167797176495157803E-4 a9 = —a—9 = 3.3521735134149972485495143293701953E-5

1234568 derivative stencil. n = 1.765, a0 = 0.0

a3 = —a—! = 0.9132066730017018501071844317880848 a2 = —a—2 = —0.3458970880904337489997562609890365 a3 = —a—3 = 0.1423752402318168875470781806014907 a4 = —a—4 = —0.051759351567246811093075274001630856 a5 = —a—5 = 0.01455611850194688853308973731674671 a6 = —a—6 = —2.4817385325786229531655586408536866E-3 a8 = —a—8 = 7.612842980494058461741370667849726E-5

12.5 Large Buffer Selective Damping Stencils

Buffer regions, where a change in mesh size takes place, are favorite sites for the generation of spurious short numerical waves. These are also regions prone to numer­ical instability. It is, therefore, necessary to add artificial selective damping to these regions. Below are optimized coefficients of several large artificial selective damping stencils designed for use in buffer regions involving change in mesh size by a factor of 2.

9-Point Stencil. a = 0.1975n

1235 stencil. в = 1.215

d0 = 0.2708886738189505 d1 = d_1 = -0.2206703054137707 d2 = d-2 = 0.11455566309052476 d3 = d-3 = -0.031235919680725313 d5 = d-5 = 2.5094190624960092E-3

1246 stencil. в = 1.075

d0 = 0.33027355532845215 d1 = d-1 = -0.25 d2 = d-2 = 0.09475341549663605 d4 = d-4 = -0.011705918179843176 d6 = d-6 = 1.815725018981057E-3

1357 stencil. в = 0.885

d0 = 0.5

dx = d-1 = -0.3062891172075045 d3 = d-3 = 0.07419885992060947 d5 = d-5 = -0.022186172045155307 d7 = d-7 = 4.276429332050351E-3

11-Point Stencil. a = 0.195n

13579 stencil. в = 0.96

d0 = 0. 5

dx = d-1 = -0.3095004246385787 d3 = d-3 = 0.08211616467055119 d5 = d-5 = -0.03036277454777355 d7 = d-7 = 9.650309477159707E-3 d9 = d-9 = -1.9032749613586592E-3

12468 stencil. в = 1.15

d0 = 0.32646005443343434 d1 = d-1 = -0.25 d2 = d-2 = 0.09831710703893635 d4 = d-4 = -0.014318492283620247 d6 = d-6 = 3.4468599861078082E-3 d8 = d-8 = -6.755019581410823E-4

12357 stencil. в = 1-3

d0 = 0.2635716529562409 d1 = d_1 = -0.21772629224768608 d2 = d_2 = 0.11821417352187955 d3 = d_3 = -0.03499568161296116 d5 = d_5 = 3.174478225315305E-3 d7 = d_7 = -4.5250436466805904E-4

12346 stencil. в = 1.4

d0 = 0.23453190899565207 dx = d_! = _0.19992274952791061 d2 = d_2 = 0.12196569374380435 d3 = d_3 = _0.050077250472089385 d4 = d_4 = 0.011317101840646436 d6 = d_6 = _5.487500822768231E-4

13-Point Stencils. a = 0.1925n

1357911 stencil. в = 1.04

d0 = 0. 5

dx = d_! = _0.31182671961098623 d3 = d_3 = 0.08793722059177961 d5 = d_5 = _0.037310514270787353 d7 = d_7 = 0.015220028715708166 d9 = d_9 = _5.094690254969648E-3 d11 = d_11 = 1.0746748292554631E-3 1246810 stencil. в = 1.225

d0 = 0.3240020968562207 d1 = d_x = _0.25 d2 = d_2 = 0.10058161761678362 d4 = d_4 = _0.016211394630950087 d6 = d_6 = 4.751848956897231E-3 d8 = d_8 = _1.4728623391755445E-3 d10 = d_10 = 3.497419683344133E-4 123579 stencil. в = 1.375

d0 = 0.2595758998570965

d1 = d_! = _0.2161210442492141

d2 = d-2 = 0.12021205007145175 d3 = d-3 = -0.037173351241118195 d5 = d-5 = 3.961825142400804E-3 d7 = d-7 = -8.500469444013784E-4 d9 = d-9 = 1.8261729233287355E-4

123468 stencil. в = 1.5

d0 = 0.22856643029671658 dx = d-1 = -0.19658662660320927 d2 = d-2 = 0.12336415951962278 d3 = d-3 = -0.053413373396790725 d4 = d-4 = 0.01316893300174682 d6 = d-6 = -9.489310483476328E-4 d8 = d-8 = 1.3262337861974504E-4

123457 stencil. в = 1.59

d0 = 0.21457119275070027 d3 = d-1 = -0.18683026262805987 d2 = d-2 = 0.12266004527546252 d3 = d-3 = -0.05945584021704768 d4 = d-4 = 0.020054358349187353 d5 = d-5 = -3.8748982424400496E-3 d7 = d-7 = 1.610010875476098E-4

15-Point Stencils. a = 0.19n

135791113 stencil. в = 1.11

d0 = 0.5

d3 = d-1 = -0.31339818418385334 d3 = d-3 = 0.0921696857561028 d5 = d-5 = -0.042740680643837763 d7 = d-7 = 0.020359003550007293 d9 = d-9 = -8.78888052362071E-3 d11 = d-11 = 3.1146836013276404E-3 d13 = d-13 = -7.156275561259213E-4

124681012 stencil. в = 1.295

d0 = 0.32236714053321097

dx = d-x = -0.25

d2 = d-2 = 0.10216769227713358

d4 = d-4 = -0.01756253154787246 d6 = d-6 = 5.840424337495861E-3 d8 = d-8 = -2.2168366108895102E-3 d10 = d-10 = 8.252438932473476E-4 d12 = d-12 = -2.3756261572031736E-4

12357911 stencil. в = 1.45

d0 = 0.25689444748256046 dt = d-1 = -0.21501278581108324 d2 = d-2 = 0.12155277625871977 d3 = d-3 = -0.038648799797586175 d5 = d-5 = 4.562916765604436E-3 d7 = d-7 = -1.1632920312828478E-3 d9 = d-9 = 3.7616806999180853E-4 du = d-u = -1.1420719564397982E-4

12346810 stencil. в = 1.58

d0 = 0.22513862785383467 dt = d-1 = -0.1946531938734711 d2 = d-2 = 0.12416686947715667 d3 = d-3 = -0.0553468061265289 d4 = d-4 = 0.014280517691395201 d6 = d-6 = -1.1996097976025642E-3 d8 = d-8 = 2.4498737887899095E-4 d10 = d-10 = -6.207867674562712E-5

1234579 stencil. в = 1.69

d0 = 0.21047015796352988 dx = d-1 = -0.18421029309503222 d2 = d-2 = 0.12295164373519486 d3 = d-3 = -0.06145360873722441 d4 = d-4 = 0.02181327728304021 d5 = d-5 = -4.569637725373214E-3 d7 = d-7 = 2.7404296254122305E-4 d9 = d-9 = -4.050340491136648E-5

1234568 stencil. в = 1.765

d0 = 0.20494238199107911 dx = d-1 = -0.1800055838379142

М = 0.4 Figure 12.22. Nozzle configuration. x = 0, throat

x

d2 = d-2 = 0.12179720514762138 d3 = d-3 = -0.06311640230450315 d4 = d-4 = 0.024628464984657864 d5 = d-5 = -6.878013857582646E-3 d6 = d-6 = 1.1454459542189518E-3 d8 = d-8 = -4.2307082037753E-5

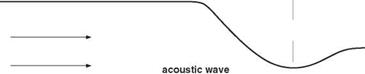
EXERCISES 12.1. In a transonic cascade, the local Mach number of the flow in the narrow passages may be close to sonic. The computation of sound propagating through such regions presents a challenging problem. To reduce the complexity of the problem, but retaining the basic physics and difficulties, a one-dimensional acoustic wave transmission problem through a nearly choked nozzle is considered.

The following characteristic scales are used to form dimensionless flow variables.

length scale = diameter of nozzle in the uniform region downstream of the throat (see Figure 12.22), D

velocity scale = speed of sound in the same region, aTO time scale = D/a

density scale = mean density of gas in the same region, pTO pressure scale = p^a2^

Consider a one-dimensional nozzle with an area distribution as follows:

= j 0.536572 – 0.198086e-(ta2)(x/0’6)2, x > 0 X = 1.0 – 0.661514e-(ln2)(x/0’6)2, x < 0 ‘

The governing equations in dimensionless form are

dp 1 dpuA dt A dx

where y = 1.4. The Mach number in the uniform region downstream of the throat is 0.4.

Small-amplitude acoustic waves, with angular frequency ы = 0.6 n, are generated way downstream and propagate upstream through the narrow passage of the nozzle throat. Let the upstream propagating wave in the uniform region downstream of the nozzle throat be

where с = 10-5. Use a computation domain of size 20,10 upstream and 10 down­stream of the nozzle throat, to calculate the distribution of maximum acoustic pres­sure inside the nozzle.

This problem can, of course, be calculated accurately if a very large number of mesh points is used. But this is not always practical. It is recommended that no more than 400 mesh points be used. In other words, use a multisize mesh to compute the solution. The boundary conditions developed in Problem 6.5 would be useful, as well.

The exact solution of this problem is available in the Proceedings of the Third Computational Aeroacoustics Workshop on Benchmark Problems, NASA CP-2000­209790, August 2000.