Characteristics of a Simple Symmetrical Loading – Elliptic Distribution

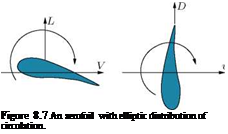
The spanwise variation in circulation is taken to be represented by a semi-ellipse having the span (2b) as the major axis and the circulation at the mid-span (k0) as the semi-minor axis, as shown in Figure 8.4, will have the lift and induced drag acting on it as shown in Figure 8.7.

From the general expression for an ellipse, shown in Figure 8.4, we have:

+ У = 1

or

(8.5)

This is the expression k = f (y) which can Aerofoil Characteristic with a More General Distribution

A more general distribution must satisfy the end conditions, namely, at the wing tips the vorticity should be zero. That is:

At y = ±b k = 0.

It is found that, for plain rectangular or slightly tapered aerofoils, the spanwise distribution does not depart drastically from elliptic distribution. The modified elliptic loading can satisfy this situation. Let:

1 + a{b

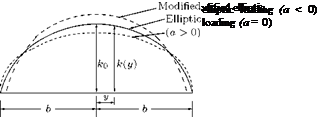The constant a can vary positively or negatively and therefore, can change the shape, but the end conditions are satisfied, as illustrated in Figure 8.8. In this figure, the area enclosed by the curves for a < 0, a = 0 and a > 0 are the same. That is, the total lift for elliptic and modified elliptic loading in this figure are the same.

8.4 The Vortex Drag for Modified Loading

The vortex drag, by Equation (8.4), is:

f Ь

Dv = pwkdy.

But for modified loading, the downwash, by Equation (8.11), is:

1 – 2k + 12k ( — b

and the vortex distribution is:

2

k = M/1 –

Substituting for w and k, we get the vortex drag as:

2	M/1 -( bj II + 4k(b) ) dy.
Dv
1 – 2k + 12k ( — b

The load is symmetrical about the mid plane, therefore the limits can be written as:

D=2 f‘ £ [‘- 2k+12k (b Я ‘V1 – (b)! (‘+4k (y)!) *.

Let y = b sin ф, therefore, dy = b cos фdф and the limits become 0 and n/2. Hence:

= —-° / [(1 – 2k) cos2 ф + (16k – 8k2) sin2 ф cos2 ф

+ 48k2 sin4 ф cos2 ф] dф.

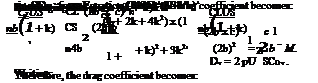These are standard integrals which result as:

the drag coefficient can be expressed as:

(8.13)

This drag coefficient for the modified loading is more than that for elliptical loading by an amount S, which is always positive since it contains X2 terms only.