Optimization Using Sensitivity Derivatives

It is often desirable to have a capability to predict the behavior of the inputs to an arbitrary system by relating the outputs to the inputs via j sensitivity derivative matrix [ !84]-( 188). while treating the system as a black box. The sensitivity derivative matrix can be used for the purpose of con­trolling the system outputs or to achieve an optimized constrained design that depends on the sys­tem outputs The objective is to generate approximations of the infinite dimensional sensitivities and to transfer these approximate derivatives to the optimizer together with the approxmiatc function evaluations. The control vanables are then updated with the sensitivity derivatives which are the gradients of the cost function with respect to the control variables. The general concepts for the sensitivity analysis can be summarized as follows (185)

The system of governing flow-field governing equations after discretization results in a system of non-linear algebraic equations

where Q is the vector of the solution variables in the flow-field governing system. X is the computational gnd and D is the vector of design variables (for example, coordinates of 3-D aerodynamic shape surface points). Hence

dR _ dRdQ dRdX Э R dD ^QdD + dXdD + dD

Similarly, aerodynamic output functions (lift. drag. Iift/drag. moment, etc.) are defined as

F = F(Q(D),X{D),D)

Hence

dF _ dFdQ. dFdX. dF dD = bQdD * bXdD + ДО

System (81) is solved for the sensitivity derivatives of the field variables, dQ/dD, which arc then substituted into the system (83) in order to obtain the sensitivity derivatives of the desired aerodynamic outputs. dF/dD. This approach is typically used if the dimension of F is greater than that of D which is seldom the case in a 3-D aerodynamic shape design.

When die number of design variables D is larger than the number of the aerodynamic output functions F. it is more economical to avoid solving for dQ/dD This can be accom­plished by using an adjoint operator approach where a linear system

)’-&)’-»

must be solved first. Here. A is a discrete adjoint variable matrix associated with the aerodynamic output functions. F. Substituting equation (84) into equation (83). it follows from equation (81) that the aerodynamic output derivatives of interest can be computed from

dF _ AT (dRdX dR dFdX dF

dD ~ A ЛЯШ + ШЇГШо + ‘Зо (85)

This quasi-analytical approach to computing sensitivity derivatives is more economi­cal and accurate than when evaluating the derivatives using finite differencing. Nevertheless, sensitivity analysis is a very costly process requiring a large number of analysis runs.

In the gradient-search optimisation approach the flow analysis cixlc must be called at least once for each design variable in order to compute the gradient of the objective function

during each optimization cycle. Since each call to the analysis code is very expensive, such an approach to design is justified only if a small number of design variables is used. In the ease of a 3-D design, this is hardly justifiable even if one uses 3-D surface geometry paramctnzation which severely constrains 3-D optimal configurations.

One of the most promising recent developments in the aerodynamic shape design opti­mization is a method that treats the entire system of partial differential equations governing the flow-field as constraints, while treating coordinates of all surface gnd points as design variables (189). This approach eliminates the need for geometry parameterization using shape functions to define changes in the geometry. Since fluid dynamic variables. Q. are treated here as the design variables, this method allows for rapid compulation of partial derivatives of the objective function with respect to the design variables. This approach is straightforward to comprehend and efficient to implement in Newton-type direct flow analysis algorithms where solutions of the equations for dQ/dD or A amount to a simple back-substitution The problem is that the classical Newton iteration algorithm is practically impossible to implement for 3-D aerody­namic analysis codes because of its excessive memory requirements when performing direct LU factorization of the coefficient matrix.

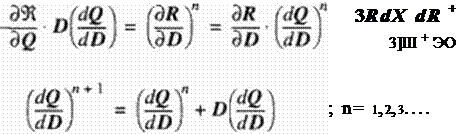Instead of using an exact New ton algorithm in the flow-analysis code, it is more cost effective to use a quasi-Newton iterative formulation or an incremental iterative. strategy (I85j. [ 190) given in the form

could be any fully-converged numerical approximation of the exact Jaco­

bian matrix.