Hybrid GA/Gradient Search Constrained Optimization

The GA has proven itself to be an effective and robust optimization tool for large variable-set problems if the cost function evaluations arc very cheap to perform. Nevertheless, in the field of 3-D aerodynamic shape optimization we arc faced with the more difficult situation where each cost function evaluation is extremely costly and the number of the design variables is relatively large. Standard GA will require large memory if large number of design variables arc used. The number of cost function evaluations per design iteration of a GA increases only mildly with the number of design variables, while increasing rapidly w ith the increased size of the initial popu­lation. Also, the classical GA can handle constraints on the design variables, but it is not inher­ently capable of handling constraint functions (198). Thus, the brute force application of the standard GA to 3-D aerodynamic shape design optimization is economically unjustifiable.

Consequently, a hybrid optimization made of a combination of the GA and a gradient search optimization or the GA and an inverse design method has been shown be an advisable way to proceed (180]. (20l]-(203). Preliminary results obtained with different versions of a hybrid optimizer that uses a GA for the overall logic, a quasi-Newtonian gradient-search algo­rithm or a feasible directions method [167) to ensure monotonic cost function reduction, and a Nelder-Mead sequential simplex algorithm or a steepest descent methodology of the design var­iables into feasible regions from infeasible ones has proven to be effective at avoiding local minima Since the classical GA docs not ensure monotonic decrease in the cost function, the hybrid optimizer could store information gathered by the genetic searching and use it to deter­mine the sensitivity derivatives of the cost function and all constraint functions (203). (180). When enough information has been gathered and the sensitivity derivatives arc known, the opti­mizer switches to live feasible directions method (with quadratic subproblem) for quickly pro­ceeding to further improve on the best design.

One possible scenario for a hybrid genetic algorithm can be summarized as follows:

• Let the set of population members define a simplex like that used in the Ncldcr-Mcad method.

• If the fitness evaluations for all of the population members docs not yield a better solution, then define a search direction as described by the Nelder-Mead method.

• If there arc active inequality constraints, compute their gradients and determine a new search direction by solving the quadratic subproblcm.

• If there are active equality constraints, project this search direction onto the subspace tan­gent to the constraints

• Perform line search.

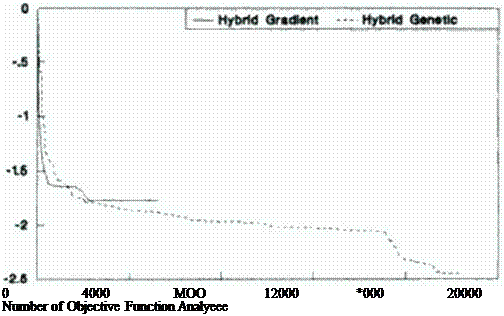
Our recent work [203]. |180) indicates that the hybrid GA can yield answers (Figure 75 and Figure 76) not obtainable by standard gradient methods at comparable convergence rates (Figure 77). This hybrid optimizer can also handle non-lincar constraint functions, although the main computational cost will be incurred by enforcing the constraints since this task will involve evaluating the gradients of the constraint functions.

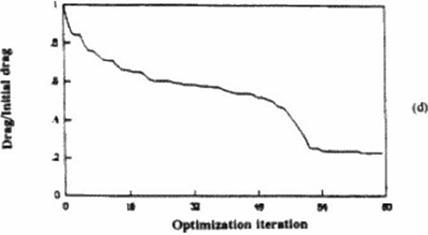
Figure 75 Our hybrid gradient search/genetk constrained optimizer keeps on improving the design even beyond the known analytic optimal solution (von Karman and Sears-Haack smooth ogives). It transformed an initially conical configuration (a) with 100% drag into a smooth ogive shape (b) with 56% drag and finally into a star-shaped spiked missile (c) with only 22% of the initial drag. Convergence history (d) shows monotonic convergence although 480 variables were optimized with a constrained volume and length of the missile [203], (180).

Starting from an initially conical body at zero angle of attack and a hypersonic oncoming flow, the hybrid G. Vgradient search constrained algorithm arrived at this smooth, cambered 3*1) lifting body with a maximized value of lift-to-drag while maintaining the initial volume and length [2031,(180].

Comparison of convergence histories of a constrained gradient search and a constrained hybrid genetic/gradient search optimizer for example shown in Figure 76, [203], 1180].

11.5 Conclusions

From the brief survey of positive and negative features of different optimization algorithms it can be concluded that:

• brute force application of gradient search sensitivity-based optimization methods is very computationally intensive and unreliable for large aerodynamic problems since they are prone to local minima.

• brute force application of genetic evolution optimizers is very computationally intensive for realistic 3-D problems that involve a number of constraints, and

• use of hybrid gcnetic/gradient search coastrained optimization algorithms offers the most reliable performance and the best convergence.