Lancaster – Prandtl Lifting Line Theory

It is a representation to improve on the accuracy of the horseshoe vortex system. In lifting line theory, the bound vortex is assumed to lie on a straight line joining the wing tips (known as lifting line). Now the vorticity is allowed to vary along the line. The lifting line is generally taken to lie along the line joining the section quarter-chord points of the wing. The results obtained using this representation is generally good provided that the aspect ratio of the wing is moderate or large, generally not less than 4.

Consider the lifting line as shown in Figure 8.10. At any point on the lifting line, the bound vortex is T(y), and there is consequently trailing vorticity of strength dT/dy per unit length shed. Note that T(y) is used to represent vortex distribution, instead of k(y). This is because it is a common practice to use both k(y) and T(y) to represent the vortex distribution.

The velocity induced by the elements of trailing vorticity of strength (dT/dy).dy at point p is given

by:

1 (dT/dy)

— ———– dy.

4n y1 – y

Total downwash at point P1 is:

The assumption in this analysis is that the downwash velocity w is small compared to the freestream velocity V, so that w/V is equal to the downwash angle e.

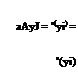Let ae (y1) be the effective angle of incidence of the wing section at point Pj. The geometrical incidence of the same section be a(y). Let both these angles be measured from the local zero-lift angle. Then:

If a<x, is the lift-curve slope of the wing section at point Pj, which may also vary across the span, the local lift coefficient CL is given by:

Ci(yi) = axae(yi).