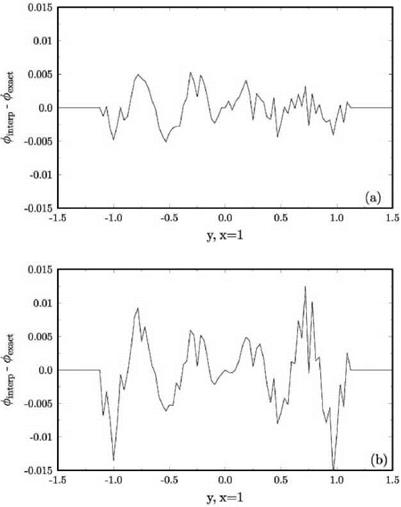
Numerical Examples: Scattering Problems
As examples to illustrate the use of overset grid method, two problems involving acoustic scattering by a rigid cylinder in two dimensions discussed in Section 13.1 will now be considered. The governing equations in Cartesian and cylindrical coordinates are Eqs. (13.1) and (13.2). They are discretized, and the numerical solutions are advanced in time by the 7-point stencil DRP scheme. The ghost point method is used to enforce the no-through-flow boundary condition.
13.3.1 Transient Scattering Problem
First, consider the scattering of an initial pressure pulse by the cylinder. For this problem, the Euler equations are solved with the initial conditions as follows:
 |
t = 0,
u = v = 0, p = ^1 — ^ + p
With a very small initial pulse amplitude (e = 10—4), the computed solution is identical to the solution of the linearized Euler equations. This cylinder scattering problem governed by the linearized Euler equation is a benchmark problem of the Second Computational Aeroacoustics (CAA) Workshop on Benchmark Problems. The exact solution given in the conference proceedings unfortunately has an error. The correct solution is provided in Appendix 13B at the end of this chapter.
|
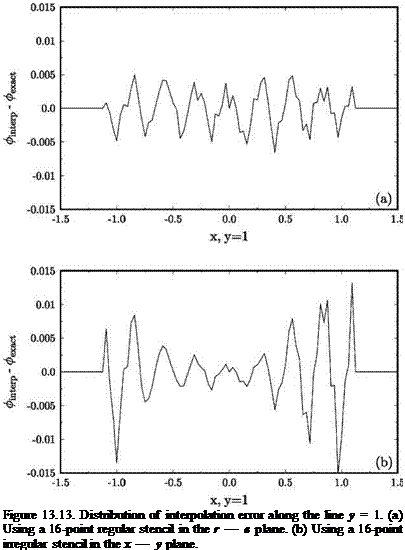
Figure 13.14. Distribution of interpolation error along the line x = 1. (a) Using a 16-point regular stencil in the r — в plane. (b) Using a 16-point irregular stencil in the x — y plane. |
Figure 13.15 shows the computed pressure contours at t = 1.6, 4.0, and 6.4. The computed contours and the contours of the exact solution are indistinguishable (the difference is less than the thickness of the contour lines). The direct acoustic pulse and the scattered pulse can clearly be seen in Figure 13.15. For a more comprehensive comparison between the numerical and exact solution, the pressure time history at three locations with Cartesian coordinates (—5, 0), (—4, 4), and (0, 5) are plotted in Figure 13.16. Plotted also in these figures is the exact solution. The differences between the exact (dashed line) and computed solution are again very small.