Effect of Downwash on Incidence

For an aerofoil:

• Geometrical incidence is the angle between the chord of the profile and the direction of motion of the aerofoil.

• Absolute incidence is the angle between the axis of zero lift of the profile and the direction of motion of the aerofoil.

When the axes of zero lift of all the profiles of the aerofoil are parallel, each profile meets the freestream wind at the same absolute incidence, the incidence is the same at every point on the span of the aerofoil, and the aerofoil is said to be aerodynamically untwisted.

An aerofoil is said to have aerodynamic twist when the axes of zero lift of its individual profiles are not parallel. The incidence is then variable across the span of the aerofoil.

To distinguish between the lift and induced drag coefficients and the incidences of the aerofoil (that is, wing) as a whole and its individual profiles, let us use CL, CDv, a for the aerofoil and CL’, CDv’, a’ for an individual profile. The coefficients CL’, CDv’ and a’ for a profile are functions of the coordinate y which defines the position of the profile. For a symmetrical aerofoil they are even functions of y, that is, to say that they are the same for +y and — y.

The lift and induced drag coefficients of the profile can be expressed as:

1 pV2 c dyC L = pVT(y)dy 2 pV2c’dyCDv’ = pwY(y)dy.

Therefore the drag and lift ratio becomes:

(8.24)

For a properly designed profile, the ratio of induced drag to lift is always small in the working range of incidence, and therefore A, which is called the angle of downwash, is a small angle. It follows that if V’2 = V2 + w2 then V = V, neglecting the second order of small quantities.

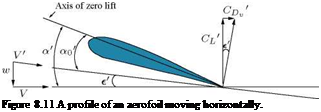
As shown in Figure 8.11, the resultant aerodynamic force on the strip is perpendicular to the direction of V and not to the direction of V. Since e’ is a small angle, the coefficient of this force is CL’. Therefore in respect to lift the strip (profile) behaves like a strip of a two-dimensional aerofoil in a relative wind in the direction of V’, that is at incidence a0′, where:

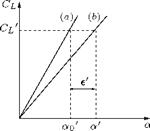
Figure 8.12 Profile lift coefficient variation with incidence (a) for a two-dimensional aerofoil, (b) for a three­dimensional aerofoil.

The angle a0′ is called the effective incidence. Thus the effective downwash is the downwash velocity that combines with the actual relative wind of speed V to produce an effective relative wind in the direction of V’.

The lift coefficient CL’ variation with incidence will be as shown by curve a in Figure 8.12. This curve is the graph proper to the profile operating as a two-dimensional aerofoil and the lift curve slope is given by:

, CL’ a0 = —: • a#0

But when the profile is operating as a part of the actual wing (that is, a three-dimensional aerofoil), the variation of CL’ with incidence will be as shown by curve b in Figure 8.12. The lift curve slope is given by:

CL

da’

It is seen that the graphs of CL’ against incidence are straight lines. In Figure 8.12, the graphs a and b are drawn with the assumption that the angle of downwash vanishes when the wind is along the axis of zero lift, that is, the axis of zero lift is assumed to be the same in the two-dimensional and three-dimensional aerofoils. With this assumption we have:

CL = a0 a0 = a! a’ • (8^26)

We know that for an actual aerofoil in a subsonic flow the main components of the drag are the profile drag and the skin friction drag. The induced drag caused by the downwash is an additional component of drag. Therefore, the total drag coefficient of the strip (profile), using Equation (8.24), is:

CD = CDo’ + c’Cl’, (827)

where CD0′ is the coefficient of profile drag for the profile.

It may be noted that the profile drag is largely independent ofincidence in the working range. Profile drag is the sum of the skin friction due to viscosity, and form drag due to the shape. The part due to skin friction is due to the no-slip caused by the viscosity of the air in the boundary layer at the surface of the body. This viscous effect is always present, but can be reduced by smoothening the surface and reducing the surface area.

The form drag due to the shape is owing to the high pressure at the leading edge and low pressure at the trailing edge (that is the low pressure in the wake). By shaping the body to reduce the wake to be of negligible thickness, that is by streamlining, the form drag can be almost eliminated.

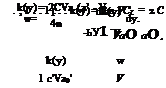Therefore:

This is the integral equation from which circulation k(y) is to be determined. Using this k(y), the lift, drag, and downwash can be determined.

Note that in general a’, a0′, C’ are functions of y, since incidence, chord and profile may vary from section to section. If the profiles are similar curves, a0′ is the same at every section, but a’ is not the same unless the sections are also similarly situated (untwisted aerofoil).

For a given wing a0′ a0′, c’ are known functions of y, and in particular for thin wings we may assume a0′ = 2n.

The following are the two problems associated with aerofoils:

• For a given circulation k(y), the form of the aerofoil and the induced drag are to be determined.

• For a given form of aerofoil, the distribution of circulation and the induced drag are to be determined.