ANN-BASED PARAMETER ESTIMATION

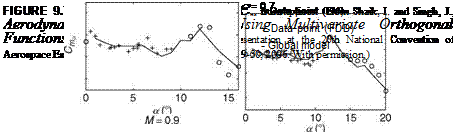9.8.1 FFNN Scheme

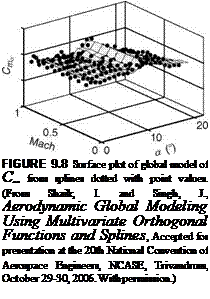We have seen that an FFNN can be used for nonlinear mapping of the input/output data. This suggests that it should be possible to use it for system identification/para – meter estimation. The FFNN works with a black-box model structure, which cannot be physically interpreted and hence the parameters, i. e., the network weights, have no interpretation in terms of the parameters of the actual system. The parameter estimation using FFNN is done in two steps: (1) the FFNN is presented with the measured data and trained to reproduce the clean/predicted responses, which are

Time (s)

FIGURE 9.9 Dynamic validation of global model of Cma from spline using 6DOF simulation. (From Shaik, I. and Singh, J., Aerodynamic Global Modeling Using Multivariate Orthogonal Functions and Splines, Accepted for presentation at the 20th National Convention of Aerospace Engineers, NCASE, Trivandrum, October 29-30, 2006. With permission.)

compared with the actual system’s responses in the sense of minimization of the output error as depicted in Figure 9.10 and (2) subsequently the predicted responses are perturbed in turn for each parameter that is to be estimated. This obtains a changed predicted response. Next, it is assumed that z = fix and the FFNN is trained to produce a clean z. Then the trained FFNN is used to produce z + Az and z — Az by changing x to x + Ax and x — Dx, and the parameter b is obtained as b = f+—x~. This is called the delta method. The estimates are obtained by averaging these respective parameter time histories, by removing some initial and some final points. The training algorithm for the FFNN is provided in Section 2.4.2.