Problem II

In problem I for a given circulation k(y), the form of the aerofoil has been found. Problem II is an inverse problem in which the form of the aerofoil is known and the circulation has to be determined. To do this we must solve the integral equation [Equation (8.29)], noting that the symmetry with respect to the median plane of the aerofoil demands that k(y) = —k(y). In terms of the eccentric angle в we can therefore write the Fourier sine series, since k(y) vanishes at the tips of the aerofoil, that is at в = 0 and в = n.

TO

k(y) = 4bU ^ ‘ An sin пв. (8.42)

1

Note that n must be an odd integer to ensure the equality of sin пв and sin n(n — в). Thus:

TO

k(y) = 4bU У ^ A2n+j sin (2n + 1)в.

n=0

This formula for k(y) is unchanged when (п — в) is written for в, and the value at the center given by в = п/2 is:

k = 4b^2A2n+1(—1)n – (8-44)

n=0

Substitution of Equation (8.43) into (8.29) gives:

b rj

> A2n+1 sin (2n + 1)в = a’———-

ТІ п J 0

^^(2n + 1)A2n+1 cos(2n + 1)фdф

n=0

b (cos ф — cos в)

At this stage it will be useful to understand the integral on the right-hand side of this equation. The integral on the right-hand side of Equation (8.45) is of the type:

In =

where n is an integer.

In terms of its principal value, let us define In as:

In = limf^0

This is physically equivalent to omitting the vorticity between (в — е) and (в + е) and then taking the limit е ^ 0 so that в remains the center of the omitted portion.

If n = 0 we have, by differentiation:

1 sin 2 (в + ф) ~^log—1—————

в—е		ве
Лф
0 (cos ф — cos в) Ґ Лф _ в+е (cos ф — cos в)
0
п

Hence:

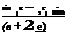
1

І0 = !ше^0 : log

sin в

It follows that we may write:

In = In — І0 cos пв =

cos пф — cos пв

—— Г——– тгЛф.

cos ф — cos в

To find the coefficients of A2n+j in Equation (8.47), we need to expand each side, and each term on the left hand side in a Fourier series, thus leading to infinite number of equations and infinite number of unknowns. To overcome this difficulty and solve Equation (8.47), we should resort to a practical method of solution, due to Glauert.

Let us replace the infinite series of Equation (8.43) by a finite series of, say, (m + 1) terms, where m is a given integer, thus giving:

m

‘У ‘ A2n+1 [(2n + 1) + sin 0] sin (2n + 1)0 = ^gag sin 0. (8.48)

n=0

This equation cannot be satisfied identically. However, if we take a particular value of 0 we get a linear equation in the coefficients A1, A3, … A2m+1. If (m + 1) particular values are assigned to 0 we get (m + 1) linear equations from which the coefficients A2n+1 can be calculated, and the values so obtained will satisfy Equation (8.48), not identically, but only at the selected points. The solution will be satisfactory if the coefficients so determined satisfy Equation (8.48) at other points within the standard of accuracy required for any particular case.

Since Equation (8.48) is satisfied in any case when 0 = 0or n, we have (m + 1) points other than these points. The chosen points are usually taken as equally spaced in 0 over the half-span. Thus if m = 3 we should take:

п 3п п п = 2 ’ Y ’ 4 ’ 8 ’

and with these values we could determine four coefficients:

A1, A3, A5, A7. (8.49)

A rough approximation is obtained by taking m = 1, and 0 = п/2, п/4. This will determine two coeffi­cients A), A3 but it must not be inferred that, comparing with Equation (8.49), A[ = A1, A’3 = A3.

If the incidence a0 has the same value a at each point on the span, Equation (8.47) shows that A2n+i is proportional to a, and if we write A2n+1 = a B2n+1, the coefficients B2n+1 are independent of incidence and may therefore be determined once for all.