Lift on the Aerofoil

Following a similar procedure we used for determining the lift and vortex drag associated with symmet­rical loading, we can show that:

b

L = pUkdy

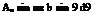pU 4bUy~]

1 2

= 2pU 2SCl,

giving the lift coefficient as:

Cl = лАЛ!,

the same as Equation (8.20a).

8.11.1 Downwash

As given by Equation (8.18), the downwash for asymmetrical loading also becomes:

U У’ иАи sin ив

w = ——————— .

sin в

But this will no longer be symmetrical as it contains even harmonics.

8.11.2 Vortex Drag

As in the case of symmetrical loading, integrating from 1 to ж, the drag becomes:

ж

Dv — 2npb2U2 ^2 nAl-

n=1

Thus the drag coefficient becomes:

2npb 2U2J2 ж=1 nAt

2 pU2S

_ n (2b)2 A 2

(2b x c) ^ П n

n—1

Ж

= лЖ ’22nAl

n—1

— лЖ [a1 + 2A2 + 3A3 + 4A4 + 5A2 +———- ].

By Equation (8.20a), A1 — Сь/(лЖ), thus:

where:

2A2 3A3

—2 – i—— 3 •

A2 + A2 + and S > 0.

Example 8.3

A monoplane weighing 73575 N has elliptic wing of span 15 m. When it flies at 300 km/h at sea level, determine the circulation around sections half-way along the wings.

Solution

Given, W — 73575 N, 2b — 15 m, V — 300/3.6 — 83.33 m/s.

The air density at sea level is 1.225 kg/m3 and in level flight, L — W.

The lift for elliptical loading, by Equation (8.6), is:

L — pUk^n 2.

Therefore, the circulation at the mid-span becomes:

2L

k0 — —–

pUnb

2 x 73575

= 1.225 x 83.33 x n x (15/2) = 61.18m2/s.

The circulation for elliptical distribution, by Equation (8.5), is:

k=kV! – (b У.

Therefore, the circulation around sections half-way along the wings, that is, at b/4, becomes: