Modelling helicopter response

Consideration of the response of helicopters to atmospheric disturbances needs to take account of a number of factors. We have seen from the simple Level 1 modelling described in Chapter 3 that the rotor response to in-plane and out-of-plane veloc­ity perturbations is distributed over the frequencies associated with the harmonics of rotorspeed. In high-speed flight the force response at the rotor hub tends to be dom­inated by the n-per-rev and 2n-per-rev components, and many studies have focused on important fatigue and hub vibratory loading problems (e. g., Refs 5.52, 5.53). Only the zero harmonic forces and the first harmonic moments lead to zero-frequency hub and fuselage response and thus affect the piloting task directly. Several studies (e. g., Refs 5.38-5.40) have concentrated on investigating factors that alleviate the fuselage response relative to the sharp bump predicted by ‘instantaneous’ models, typified, for example, by eqn 5.77. Rotor-fuselage penetration effects coupled with any gust ramp characteristics tend to dominate the alleviation with secondary effects due to rotor dynamics and blade elasticity. Rotor unsteady aerodynamics can also have a significant influence on helicopter response, particularly the inflow/wake dynamics (see Chapter 3). An important aspect covered in several published works concerns the cyclo-stationary nature of the rotor blade response (Refs 5.42, 5.43, 5.54, 5.55). Essentially, the radial distribution of turbulence effects varies periodically and the gust velocity environments at the rotor hub and rotor blade tip are therefore substantially different. If a helicopter is flying through a sinusoidal vertical gust field with scale L and intensity Wgm, then the turbulence velocities experienced at the rotor hub and blade tip are given by the expressions

wgh)(t) = wgm sin j (5.81)

(t) 12n Vt 2n R }

wgt) = wgm sin j —————- — cos (5.82)

where Vis the combined forward velocity of the aircraft and gust field. Response studies that include only hub-fixed turbulence models (eqn 5.81) and assume total immersion of the rotor at any instant clearly ignore much of the local detail in the way the individ­ual blades experience the gust field. At low speed with scales O(R), this approximation becomes invalid, and recourse to more detailed modelling is required. Assuming the gust field varies linearly across the rotor allows the disturbance to be incorporated as an effective pitch (roll) rate or non-uniform inflow component. This level of approxi­mation can be regarded as providing an interim level of accuracy for gust scales that are larger than the rotor but that still vary significantly across the disc at any given time. In Ref. 5.56, a study is reported on the validity of various approximations to the way in which rotor blades respond to turbulence, suitable for incorporation into a real-time simulation model. The study concluded that the modelling of two-dimensional turbu­lence effects is likely to be required, and that approximating the turbulence intensity over a whole blade by the value at the 3/4 radius would provide adequate levels of accuracy.

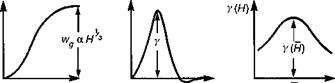
In addition to characterizing the atmospheric disturbance, the SDG approach, augmented with the transient wavelet analysis, provides a useful insight into helicopter response. The concept of the tuned response is illustrated in Fig. 5.35. Associated with each ramp gust input (Fig. 5.35(a)) we assume the response variable of interest has a single dominant peak, of amplitude у, as shown in Fig. 5.35(b). If the helicopter model is excited with each member of the family of equi-probable gusts, according to the von Karman PSD, then we find, in general, that the response peak function takes the form given in Fig. 5.35(c). There exists a tuned gust length H that produces a ‘resonant’ response from the helicopter. This transient response resonance is the equivalent of the resonance frequency in the frequency domain representation, and can be used to quantify a helicopter’s ride qualities.

H-

(a)