RNN for Parameter Estimation
The idea is to estimate the parameters of a dynamic system
![]() 5c = Ax + Bu; x(0) = x0
5c = Ax + Bu; x(0) = x0
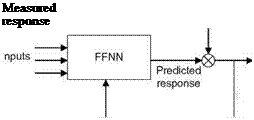
 |
Error
![]()
|
|
|
|
|
|
|
|
|
|
|
|
j=1
![]() + hi, j=i
+ hi, j=i
and since bi = f (Xi), and Xi = (f-1)’b,• dPi
we have, (f 1)’/3,• = —; hence
Comparing expressions from Equations 9.76 and 9.77 to Equation 9.80, the expressions for the weight matrix W and the bias vector b are obtained as
![Подпись: X21 X2X1 0 0 EUX1 0 EX1X2 X22 0 0 uX2 0 0 0 X21 X2X1 0 uX1 0 0 X1 X2 P X2 0 EUX2 X1 u EX2U 0 0 Eu2 0 0 0 X1 u EX2U 0 u2 EX 1x1 X]X 1X2 EX2X1 X]X2X2 EX 1U X]X 2И](/img/3131/image512_0.gif) (9.83)
(9.83)
(9.84)
The algorithm for parameter estimation of a dynamic system is given as follows: (1) as the measurements of X, X, and u are available for a certain time interval T, compute W matrix and bias vector b; (2) choose initial values of b randomly; and (3) solve the following differential equation.
Since bi = f (X;) and the sigmoid nonlinearities are known, by differentiating and simplifying, we get
Integration of Equation 9.85 would yield the solution to the parameter-estimation problem posed in equation error/RNN structure. Proper tuning of A and p is
essential. Often l is chosen as a small number, i. e., less than 1.0. The value of p is chosen such that when xt (of RNN) approaches ±1, f approaches ± p.











