Scaling Parameters for the Flexible Wing Framework

As previously discussed in Section 1.2, scaling parameters resulting from dimen­sional analysis help identify key characteristics of the model, via Buckingham’s П-theorem, and also reduces the number of involved parameters to the sufficient number of combinations [333], [447]-[449]. Under certain circumstances, the result obtained from the dimensional analysis can be reduced to a simpler relationship, with a reduced number of arguments, as a property of the special problem under consideration. The non-dimensional parameters arising from such a scaling analysis can identify similarity variables, which can be of critical value even if a complete mathematical solution is missing [447].

Generally for a flapping rigid wing framework (as discussed in Chapter 3), two non-dimensional parameters, such as Reynolds numbers and reduced frequency or the Strouhal number, are manifest in the governing equations of the fluid. For the field of flexible flapping wing aerodynamics, numerous efforts using scaling argu­ments have increased our knowledge of the complex interplay between flexibility and the resulting aerodynamics. However, depending on the type of model and on the governing equations, the resulting set of scaling parameters may vary. For instance, for flexible flapping wings, Shyy et al. [450] considered the flapping wing aeroelas – tic system based on the Navier-Stokes equation coupled with out-of-plane motion

of an isotropic flat plate. Ishihara et al. [451] [452] introduced the Cauchy num­ber that describes the ratio between the fluid dynamic pressure and elastic reaction force from the scaling argument (the Navier-Stokes equation along with the linear isotropic elasticity equations) and presented the correlation between time-averaged lift and the Cauchy number. Thiria and Godoy-Diana [453] and Ramananarivo, Godoy-Diana, and Thiria [454] introduced the elastoinertial number, using scaling arguments to define the ratio between the inertial forces and the elastic restoring forces, and showed the correlation between time-averaged thrust and the elastoin – ertial number, based on flight velocity measurement using a self-propelled flapping flyer with flexible wings in air. Since the density ratio between the air and the wing is high (~O(103)), the elastic deformation of the wing was mostly balanced by the wing inertia. Furthermore, Ramananarivo et al. [454] linked the cubic non-linear damping term due to the aerodynamics to the effects of flexibility in the aerody­namic performance. However, it is very difficult for any one study to cover all of the parameter-space of the flapping flexible wing system in which we are interested. For example, the effects of density ratios on the force generation of flexible flapping wings have not been adequately addressed. Ideally the parameter-space involving the scaling parameters for the fluid-structure interactions should be mapped out in a systematic fashion to understand the impact of flexibility and the density ratio on the force generation and propulsive efficiency of coupled systems. However, as is shown next, the number of dimensionless (scaling) parameters involved is large, making it practically impossible to examine all combinations. Consequently, insight is needed so that efforts can be directed toward creating a suitable combination of these scaling parameters.

We considered the relevant physical quantities related to the system of flexible flapping wing fluid dynamics proposed in Shyy et al. [450] [455] and Kang et al. [351]. There are 13 variables (see Figure 3.5a): the density, p, and the viscosity, л, of the fluid; the reference velocity, Uref, of the fluid flow field; the half-span, R, the mean chord, cm, and the thickness, hs, of the wing geometry; the density, ps, the Young’s modulus, E, and the Poisson’s ratio, v, of the wing structure; the flapping (plunging) amplitude, фа (ha), the flapping frequency, f, and the geometric AoA, a; and finally the resulting aerodynamic force, F. Three fundamental dimensions lead to 10 non-dimensional parameters. With p, Uref, and cm as the basis variables to independently span the fundamental dimensions, the dimensional analysis leads to the non-dimensional parameters shown in Table 4.2. The resulting set of non­dimensional parameters includes most of the well-known parameters in the flapping wing aerodynamics community; however, there are other sets of non-dimensional parameters. More importantly, some of these dimensionless parameters scale with a flyer’s physical dimensions in different ways. As pointed out in Section 1.2, the different scaling relationships between the various dimensionless parameters and size, speed, and other parameters of flapping wings pose fundamental difficulties in utilizing a laboratory model of different sizes: as the physical dimension and speed of a wing change, the scaling parameters vary differently, making it virtually impossible to conduct experiments capable of maintaining dynamic similarity.

Although Table 4.2 offers a complete set of dimensionless parameters based on the dimensional quantities selected, alternative parameters can be derived by combining these dimensionless parameters. For example, the advance ratio J given

by Eq. (3-14) results from the Strouhal number. Another example is the effective inertia П0 (Eq. 4-24),

П0 = p *h* (k/n)2, (4-24)

which is used frequently later to discuss the scaling of aerodynamic forces of a flexible wing, is a combination of p*, h*, and k. Two other non-dimensional param­eters that prove to be important are the frequency ratio, f/f1, which is the ratio between the motion frequency and the first natural frequency of the wing, and the non-dimensional tip deformation parameter, у, which scales with the aerody­namic performance. The relation between the non-dimensional parameters shown in Table 4.2 and these two parameters is derived in Section 4.5. Furthermore, additional dimensionless parameters arise as the scope of the mechanical system broadens. As discussed by Shyy et al. [450], if an anisotropic shear deformable plate is considered for the wing, an additional dimensionless parameter appears that describes the ratio between rotational inertia forces and aerodynamic forces. This effective rotational inertia parameter П2 is defined as

П2 = Ib/ (pUf, (4-25)

where IB is the mass moment of inertia. The effects of the twist on the aerodynamic performance have been considered many times in the literature [24].

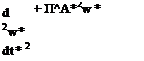The flexible wing structure can be modeled locally as a beam (see Eq. (4-1)) that oscillates in time due to its flexibility under the aerodynamic loading. Following the same non-dimensionalization process as in Chapter 3, Eq. (4-1) becomes

where special care is given in the direction of the wing bending, because the correct length scale for the spanwise bending is the half-span R and not the chord cm. The
correction factor that arises is expressed as (l/cm), where (l/cm) = 1 for the chordwise flexible airfoil case (Section 4.4.2.1) and (l/cm) = AR for the spanwise flexible wing case (Section 4.4.2.2) or isotropic Zimmerman wing case (Section 4.4.2.3) where AR is the aspect ratio of the wing: for the 3D wings the bending motion is aligned with R, so that a factor of AR is required to renormalize the transverse displacement. All non-dimensional parameters appearing in Eq. (4-26) are consistent with the parameters listed in Table 4.2. The effective stiffness П1 = Eh*3/{12 pUr2ef} [450] gives the ratio between the elastic bending forces and the fluid dynamic forces. The equivalent effective stiffness for the plate and membrane can be found easily; that is, Eh*3/{12(1 – v2)pUr2ef} and Eh*7(12pU2ef), respectively. The coefficient of the inertial term in Eq. (4-26), abbreviated as the effective inertia, is П0. Finally, the force coefficient is then given by a to-be-determined relation

CF = Ф(Re, AR, h*, p, П k, St). (4-27)