The Lift for Elliptic Loading

From Equation (8.43), we have:

The lift is given by:

/+Ь k(y)dy.

With Equation (8.50), the lift becomes:

L = 4pb2U2 A2n+1 sin (2n + 1)O J0

sin OdO.

For n = 0:

L = 4pb2U 2( A1 sin2 OdO ■J0 = 4pb2U 2A12 = 2 pU2(2b)2nA1.

Thus the lift coefficient for the whole aerofoil is:

Cl

L 2pU2 (2b x c) 2 pU2(2b)2nA1 1 pU2 (2b x c)

= nA

2b 1 c

That is:

Cl = nA1Al. (8.51) Thus the coefficient A1 = CL/(nAi), and this gives a check on the theoretical value of A1, with which Cl can be determined by wind tunnel measurements. For elliptical loading all the A2n+1 are zero except A1, therefore, Equation (8.44) gives the circulation as: k0 = 4b UA1. (8.52)

From Equations (8.51) and (8.52), we get the lift coefficient as:

Cl

nk,0-^R 4b U.

If the incidence a is the same at every point of the wing span, by Equation (8.46), A1 is proportional to a. From Equation (8.51), we have:

Cl = nA1Al.

Lift and Drag Calculation by Impulse Method

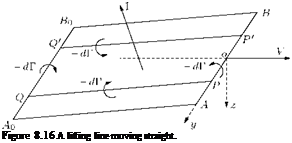Let us consider an aerofoil, regarded as a lifting line AB, started from rest and which moves in a straight line. Let the velocity be V at time t. Let at time t the starting vortex be assumed to be A0B0, as shown in Figure 8.16.

Let us assume that the wake ABA0B0 remains as a rectangular sheet, as shown in Figure 8.16. If P is the point (0, y, 0) and Q is the point (-l, y,z). The flow from point P reaching the line A0 B0 experiences a circulation of – dk(y) [Equation (8.1)]. Therefore the whole wake may be regarded as resulting from the superposition of vortex rings, a typical one being PP’ QQ of circulation – dk(y).

Let PQ = h. The area of the ring is 2yh. If n is the unit normal to a small area dS separating points P and Q, the impulse on this area due to impulsive pressure is:

—npфPdS at P and + npфQdS at Q,

where:

ФQ – фp = drc = k,

where c is any circuit joining points P and Q and not intersecting the plane containing P and Q. Thus the resultant linear impulse on the system is the vector:

I = I p (фq — фP) ndS = I pkndS = pkSn.

Js J S

Thus the impulse for the area (2yh) of the vortex ring, with n as the unit normal to the plane rectangle, is:

dl = p [—dk(y)] 2yhn = pdk(y) ■ 2y (kl + iz),

since —hn = kl + iz, by geometry. The impulse I of the whole wake is:

[ 2ydk(y) = f ydk(y) = [yk(y)] + — f k(y) dy.

J OA J BA J-b

Thus:

/

+b

p (kl + iz) k(y) dy.

The time rate of change of the impulse gives the force. Therefore the aerodynamic force is dl/dt and dl/dt = V, while dz/dt = w, the normal velocity at Q, which by symmetry of the ring is equal to the downwash velocity at P. Thus the aerodynamic force is:

/

+b f‘ +b

pVk(y) dy — i pwk(y) dy,

b J —b

which consists of the same lift and induced drag as were calculated by Prandtl’s hypotheses.

The method of the impulse is applicable whatever the form of the wake.