Rolling Moment

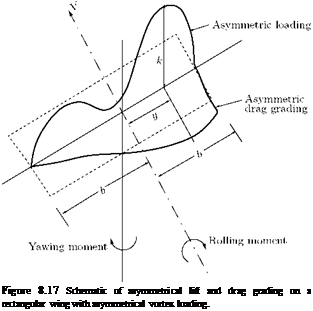Let us consider a rectangular wing with an asymmetrical lift grading and the corresponding drag grading, as shown in Figure 8.17.

The lift acting on any section of spanwise length Sy at a distance y from the centerline (ox-axis) will produce a negative increment of rolling moment equal to:

ALr = —lydy, (8.59)

where l is the lift grading given by l = pVk.

The total moment becomes:

b /• b

ly dy = — I pVk y dy.

b J—b

Substituting k = 4bV^2 An sin uB and expressing y = b cos в, we get:

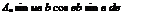
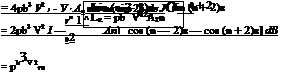Lr = 4pbV2 / J2

The rolling moment is also given by:

1 2

Lr = 2 pV2SCLRb,

where CLr is the rolling moment coefficient. Therefore:

Lr

pV 2Sb

pb3V 2A2n 2pV2 (2b x c) b 2nA2b2 2b x c 2nA2(2b)2 4 x 2b x c n 2b

2 — A2.

2c

2b

But — = JR, therefore:

c