Yawing Moment

The asymmetrical drag grading across the span, shown in Figure 8.17, gives rise to yawing moment N. The contribution of the vortex drag of an element of span dy, at a distance y from the oz-axis is:

AN = dvydy,

where dy is the vortex drag per unit span and dv = pwk. Integration over the whole span gives the yawing moment as:

b pb

dvydy = I pwkydy.

b J-b

Inserting the series expressions for the circulation k and downwash w, and changing the limits and variables from Cartesian to polar, we get:

Ґ У’ nAn sin ив

pV—————— 4bV у An sin neb cos ebsin ede

Jo P sin в ^ n

= —4pb3V2 ^ ‘ nAn sin nQ ‘У ‘An sin пЄ cos ede.

0

The yawing moment can also be expressed as:

where CN is the yawing moment coefficient. Thus:

CN = ‘S^nAn sin nQ ‘У ‘An sin nQ cos QdQ.

0

Multiplying these series for a few terms, we can express the general solution as:

since all terms other than those with coefficients which are products of A1A2, A2A3, A3A4, etc. vanish on integration.

Example 8.4

A symmetrical profile of aspect ratio 7 and chord 1.5 m flying at 200 km/h at sea level is suddenly subjected to a downwash of 2.4 m/s. If the horizontal tail of span 3 m and chord 0.6 m is 5 m aft of the aerodynamic center of the profile, determine the tail deflection required to counter the pitching moment caused by the sudden downwash.

Solution Given, = 7, c = 1.5 m, V = 200/3.6 = 55.56 m/s, w = 2.4 m/s, lt = 5 m. The planform areas of the profile and horizontal tail are:

w V 2.4 55.56 0.0432.

a

Thus:

Cl = n x 7 x 0.0432 = 0.95.

The lift generated by the profile is:

12 L = – pV 2SCl = 1 x 1.225 x 55.562 x 15.75 x 0.95 2 = 28290.12 N. For symmetrical profile, the aerodynamic center is at c/4 from the leading edge, therefore the pitching moment about the leading edge becomes: c Mie = L x 4 = 28290.12 x — 4 = 10608.8 N-m.

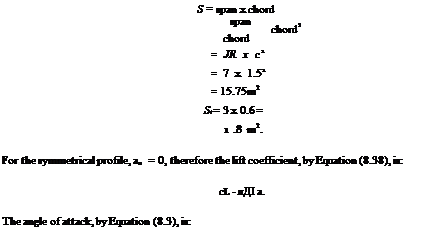Note that the pitching moment caused by the downwash is nose-down (negative). Therefore, the horizontal tail has to generate a downward lift, resulting in a pitching moment which is positive (to counter the nose – down moment). This calls for an upward deflection of the horizontal tail by 14.28°.