Lifting Surface Theory

Lifting surface theory is a method which treats the aerofoil as a vortex sheet over which vorticity is spread at a given rate. In other words, the aerofoil is regarded as a surface composed of lifting elements. This is different from the lifting line theory, discussed in Section 8.7. The essential difference between the lifting surface theory and lifting line theory is that in the former the aerofoil is treated as a vortex sheet, whereas in the latter, the aerofoil is represented by a straight line joining the wing tips, over which the vorticity is distributed.

8.12.1 Velocity Induced by a Lifting Line Element

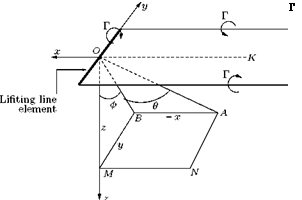
Let us consider a horseshoe vortex of infinitesimal span ds and circulation Г, as shown in Figure 8.18. The origin is at the mid-point of the span and the x-axis parallel, but opposed in sense, to the arms I, I’ of the horseshoe. Let us calculate the induced velocity at the point A (x, y, z). For this let us first consider a single semi-infinite vortex OK of circulation Г, in the same sense as the circulation about arm I. Let the velocity induced by vortex OK at A be (u,v, wj). If this vortex OK were shifted to coincide with

I the induced velocity would be, by Taylor’s theorem:

because the effect on the velocity is the same as if no shift were made, and the y-coordinate of A were increased by 2ds.

The vorticity direction on arm I’ is opposite to that on arm I, therefore the velocity induced by arm I’ at A would be:

Therefore the total velocity induced at A by the pair I, I’ is:

du1 9v1 9w1

—- ds, — ds, ———- ds.

dy dy dy

Projecting A on the plane x = 0, the plane y = 0 and the z-axis we get the points B, N, M shown in Figure 8.18. Let OB = n, OA = r.

The vortex OK induces a velocity q1 perpendicular to plane OAB. Thus:

U1 = 0, v1 = —q1 cos ф, w1 = q1 sin ф,

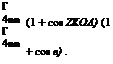where by Equation (5.50):