Blenk’s Method

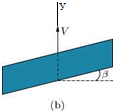
This method is meant for wings of finite aspect ratio and is based on the lifting line theory of Prandtl, discussed in Section 8.7, hence limited to aerofoils moving in the plane of symmetry and with a trailing edge which could be regarded as approximately straight. This method considers the wing as a lifting surface, that is to say the wing is replaced by a system of bound vortices distributed over its surface rather than along a straight line coinciding with the span. However, this method has the limitation that the wing is assumed to be thin and practically plane. The shapes considered are shown in Figure 8.21

In all cases the arrow indicates the direction of motion. The angle в, which is considered to be small, is the angle between a leading edge and the normal, in the plane of the wing, to the direction of motion.

In all the cases in Figure 8.21 it is assumed that the bound vortices are parallel to the leading edge, so that in particular for wing shape (c) the bound vortex lines are also arrow-shaped.

The following are the two main approaches employed in Blenk’s method:

Figure 8.21 Some wing shapes meant for Blenk’s method; (a) rectangular wing moving in the plane of symmetry, (b) a skew wing in the shape of a parallelogram moving parallel to its shorter sides, (c) a symmetrical arrow-shaped wing (sweep-back), (d) rectangular wing side-slipping.