EPILOGUE

More than a dozen parameter-estimation methods are treated with several example cases and many exercises in Ref. [1]. Various aspects of SID are treated in Ref. [41]. The ML/output error approach is found to be very popular for aircraft parameter estimation. In Ref. [42], a new compact formula for computing the uncertainty bounds for the OEM/MLE estimates is given. It utilizes the information matrix, output sensitivity, the covariance of the measurement noise, and the autocorrelation of the residuals. KF algorithms have a wide variety of applications: state estimation, parameter estimation, sensor data fusion, and fault detection. Numerically reliable algorithms are treated in Refs. [8,15]. The approaches for state/parameter estimation using fuzzy logic-based methods and derivative free KF are relatively new and these would find increasingly more application in aerospace vehicle data analysis.

EXERCISES

9.1 Why would a ‘‘long’’ (in terms of the order of the model) AR model be required for a given data set compared to LS or ARMA model for the same data set?

9.2 Why are Cm and Cn identical in the case study of the AGARD SDM?

9.3 There are two distinct parts in the expression of FPE (Table 9.1). Explain the significance of each with respect to the order ‘‘n.’’

9.4 What is the significance of the fudge factor in assessing the uncertainty of the parameter estimates?

9.5 Compare features of the method for the determination of neutral and maneuver points by classical and parameter-estimation methods.

9.6 Given y(k) = b0u(k) + bu(k — 1) — aiy(k — 1), interpret this recursion, obtain TF form, and comment.

9.7 Give the significance of the elements of matrix W and vector b in RNN parameter-estimation scheme.

9.8 What is the significance of using (residual) error time-derivative in the FCV?

9.9 Why are the results of FKF with 4 rules almost similar to those with 49 rules?

9.10 Comparing the concepts of EKF and DFKF, what is really emphasized by the differences between the two approaches?

9.11 Can you guess what types of ‘‘errors’’ can be defined for SID problems before one can specify a cost function for optimization?

9.12 Why is the choice of an adequate model structure important in SID problem? 9.13 Compare Baye’s theorem of Appendix B and MLE; what is the fundamental difference between the two from the probabilistic point of view? 9.14 Generate simulated data using the state and aerodynamic models of aircraft dynamics (Chapters 3 through 5):

Parameters True Values CD0 0.046 CDa 0.543 CD8e 0.138 CL0 0.403 CLa 3.057 CL8e 1.354 c v-‘m0 0.010 c v-‘ma -0.119 c ^mq -1.650 Cm8e – 0.571

V a q в

—— Cd – g sin(0 – a) m -Щ} Cl + 77 cos(0 – a) + q mV V

У

q

The aerodynamic model is taken as

Cd Cl c y~-m

Time histories of variables V, a, q, в, V, a, q, в, 8e and coefficients Cd, Cl, and Cm should be generated using the given equations with sinusoidal input 8e = A sin(U); A = 1, в = 0 : p/8 : np, and n = 25. For the simulation, true values of aerodynamic coefficients are given as in the above table. The other parameters related to simulated aircraft are C = 10 m, S = 23.0 m2, m = 7000 kg, Iy = 50000 kg m2, V = 100 m/s, q = 5000 kg/m s2, and g = 9.81 m/s2. The initial value of a, q, and в can be taken as 0.1 rad, 0.0 rad/s, and 0.1 rad, respectively. You can generate 200 data samples by simulation for analysis. For a given set of the true values do the following:

1. Generate the time histories of variables V, a, q, в, V, a, q, в, 8e and coefficients Cd, Cl, and Cm with sinusoidal input data and SNR = 100 (almost no noise!), using MATLAB.

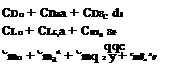2. Use ANFIS to predict the aerodynamic coefficients. Write the MATLAB code based on the theory of ANFIS discussed in Section 9.9.1.

3. Use the delta method to estimate the aerodynamics derivatives (Section 9.8.1).

If the code is written properly, you should be able to get the results given in the solution manual.

9.15 What is the fundamental relation between the information matrix and the covariance matrix? What is the significance of this relationship with reference to accuracy of data/estimates?

9.16 How would you transform the value of Cnp estimated from flight data to a reference value?

9.17 A parametric relation between the measured data and the parameter to be estimated is given as

z = xb + n

Determine the corresponding covariance relations.

9.18 If we attempt to include Cm_ in the longitudinal SP model for identifica – tion/estimation, what difficulty would be encountered?

9.19 In LAM analysis via data partitioning method, what is the main requirement for length of the data/number of data points from the point of view of consistency of the estimates?

9.20 What is model error?

9.21 What do the Gaussians (probability density) in Kalman and maximum likeli­hood really represent?

9.22 Kalman filter is obtained by parameterization of a Gaussian distribution. What is this parameterization?

9.23 In essence the KF is an implementation of the Bayes filter (see Appendix B). Explain this.

9.24 If in a KF some consecutive measurements are not available, what would be the status of the state-covariance matrix? What is the measure of this growth?

9.25 If a variable with Gaussian pdf is passed through a nonlinear function, will it retain its Gaussianness? How would you compute the pdf of the transformed values?

9.26 Although EKF is applicable to nonlinear systems, the pdf involved in EKF is (still) a multivariate Gaussian. Why?

9.27 In principle, will the DFKF be more accurate than the EKF? If so, why?

9.28 Are the sigma points determined stochastically or deterministically?